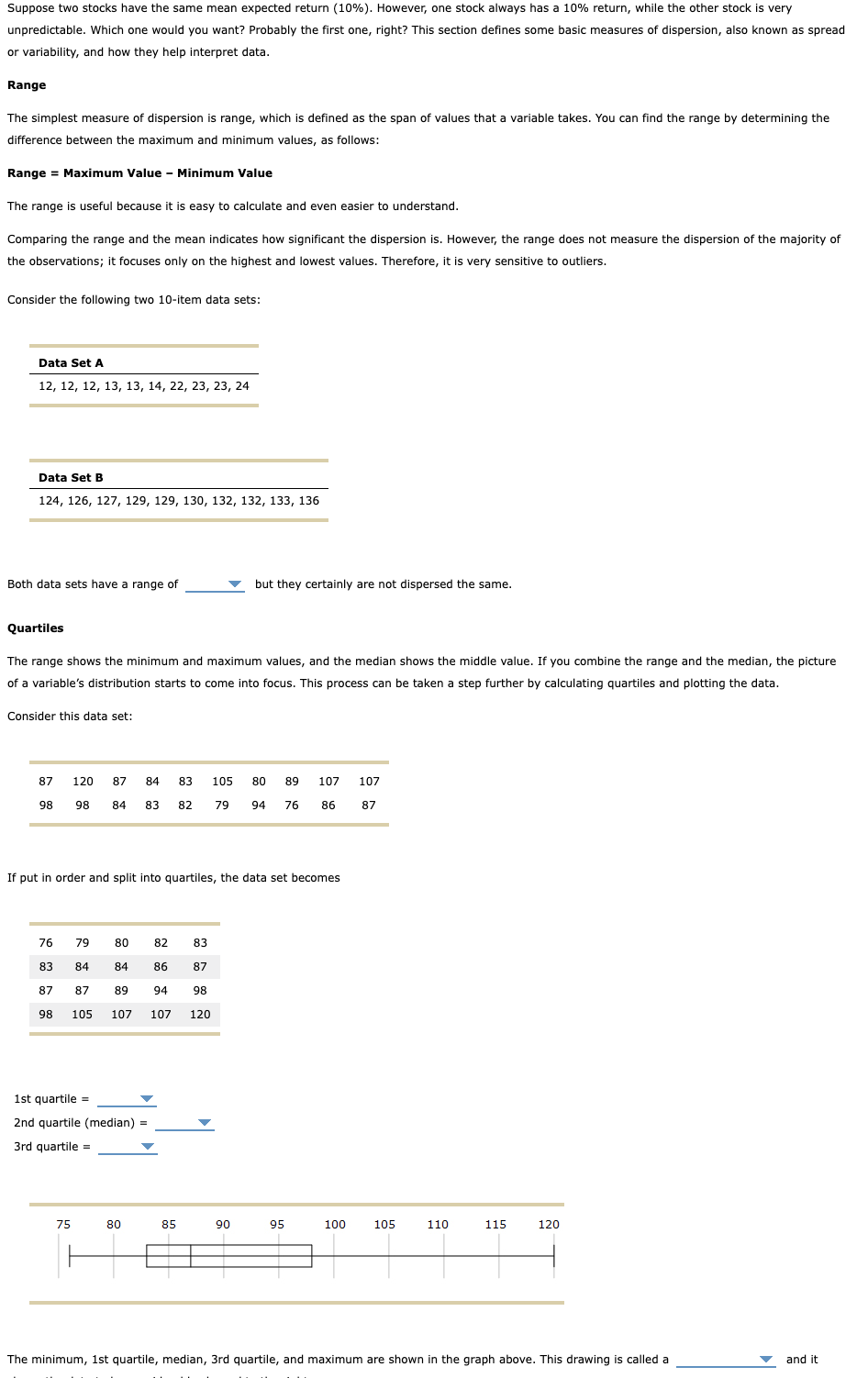
Suppose two stocks have the same mean expected return ( 10%). However, one stock always has a 10% return, while the other stock is very unpredictable. Which one would you want? Probably the first one, right? This section defines some basic measures of dispersion, also known as spread or variability, and how they help interpret data. Range The simplest measure of dispersion is range, which is defined as the span of values that a variable takes. You can find the range by determining the difference between the maximum and minimum values, as follows: Range = Maximum Value - Minimum Value The range is useful because it is easy to calculate and even easier to understand. Comparing the range and the mean indicates how significant the dispersion is. However, the range does not measure the dispersion of the majority of the observations; it focuses only on the highest and lowest values. Therefore, it is very sensitive to outliers. Consider the following two 10 -item data sets: Both data sets have a range of but they certainly are not dispersed the same. Quartiles The range shows the minimum and maximum values, and the median shows the middle value. If you combine the range and the median, the picture of a variable's distribution starts to come into focus. This process can be taken a step further by calculating quartiles and plotting the data. Consider this data set: If put in order and split into quartiles, the data set becomes 1st quartile = 2nd quartile (median) = 3rd quartile = Suppose two stocks have the same mean expected return ( 10%). However, one stock always has a 10% return, while the other stock is very unpredictable. Which one would you want? Probably the first one, right? This section defines some basic measures of dispersion, also known as spread or variability, and how they help interpret data. Range The simplest measure of dispersion is range, which is defined as the span of values that a variable takes. You can find the range by determining the difference between the maximum and minimum values, as follows: Range = Maximum Value - Minimum Value The range is useful because it is easy to calculate and even easier to understand. Comparing the range and the mean indicates how significant the dispersion is. However, the range does not measure the dispersion of the majority of the observations; it focuses only on the highest and lowest values. Therefore, it is very sensitive to outliers. Consider the following two 10 -item data sets: Both data sets have a range of but they certainly are not dispersed the same. Quartiles The range shows the minimum and maximum values, and the median shows the middle value. If you combine the range and the median, the picture of a variable's distribution starts to come into focus. This process can be taken a step further by calculating quartiles and plotting the data. Consider this data set: If put in order and split into quartiles, the data set becomes 1st quartile = 2nd quartile (median) = 3rd quartile =