1. Suppose u() = ln(). Show that the inverse function I(i) = i^1, the Lagrange multiplier = ^1, the optimal attainable wealth is W = Z^1B1, and the optimal objective value is ln() E[ln( Z/B1 )]. Compute these expressions and solve for the B1 optimal trading strategy in the case where N = 1, K = 2, r = 1/9, S0 = 5,S1(1) = 20/3 ,S1(2) = 40/9 , and P(1) = 3/5. Note that Z = Q/P , where Q is the risk neutral
   

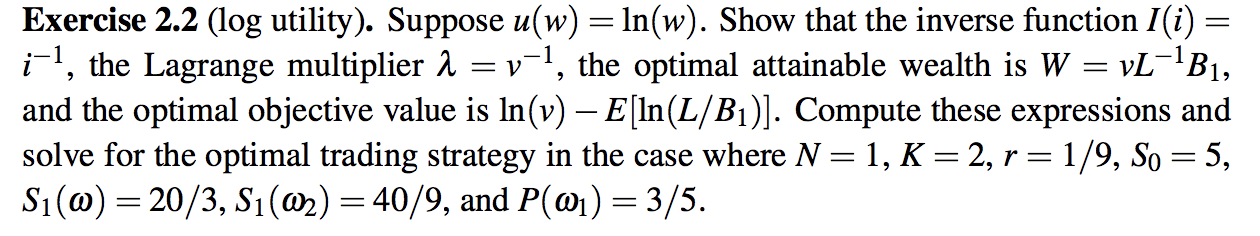
Exercise 2.2 (log utility). Suppose u(w) =1n(w). Show that the inverse function 1(i) = i'l, the Lagrange multiplier l = 121, the optimal attainable wealth is W = vL'lBl, and le optimal objective value is ln(v) E [In (L/ 31)]. Compute uese expressions and solve for the optimal trading strategy in the case where N = l, K = 2, r = 1/9, S0 = 5, 51(60) 2 20/3, 81(02) 2 40/9, and 13(01): 3/5