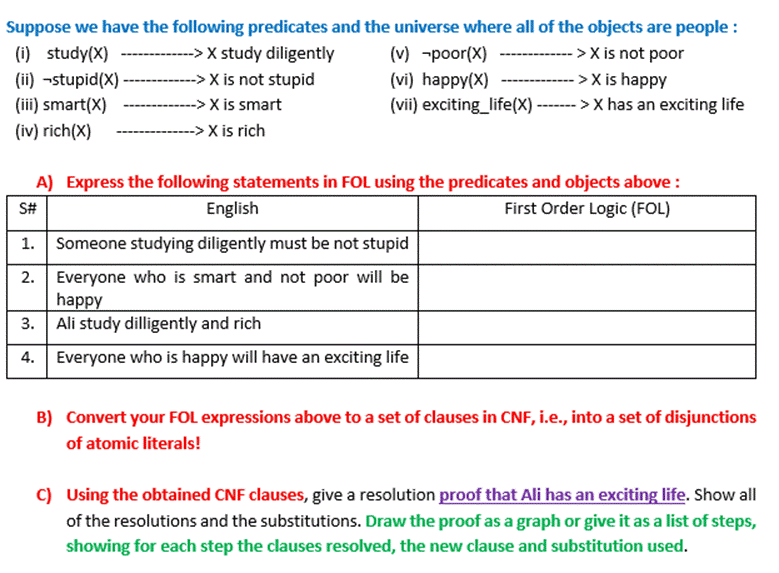
Suppose we have the following predicates and the universe where all of the objects are people : (i) study(X) -------------> X study diligently (v) poor(X) --> X is not poor (ii) -stupid(X). -> X is not stupid (vi) happy(x) ->X is happy (iii) smart(X) --> X is smart (vii) exciting_life(X) -------> X has an exciting life (iv) rich(x) -> X is rich --------- A) Express the following statements in FOL using the predicates and objects above: First Order Logic (FOL) S# English 1. Someone studying diligently must be not stupid 2. Everyone who is smart and not poor will be happy 3. Ali study dilligently and rich 4. Everyone who is happy will have an exciting life B) Convert your FOL expressions above to a set of clauses in CNF, i.e., into a set of disjunctions of atomic literals! C) Using the obtained CNF clauses, give a resolution proof that Ali has an exciting life. Show all of the resolutions and the substitutions. Draw the proof as a graph or give it as a list of steps, showing for each step the clauses resolved, the new clause and substitution used.