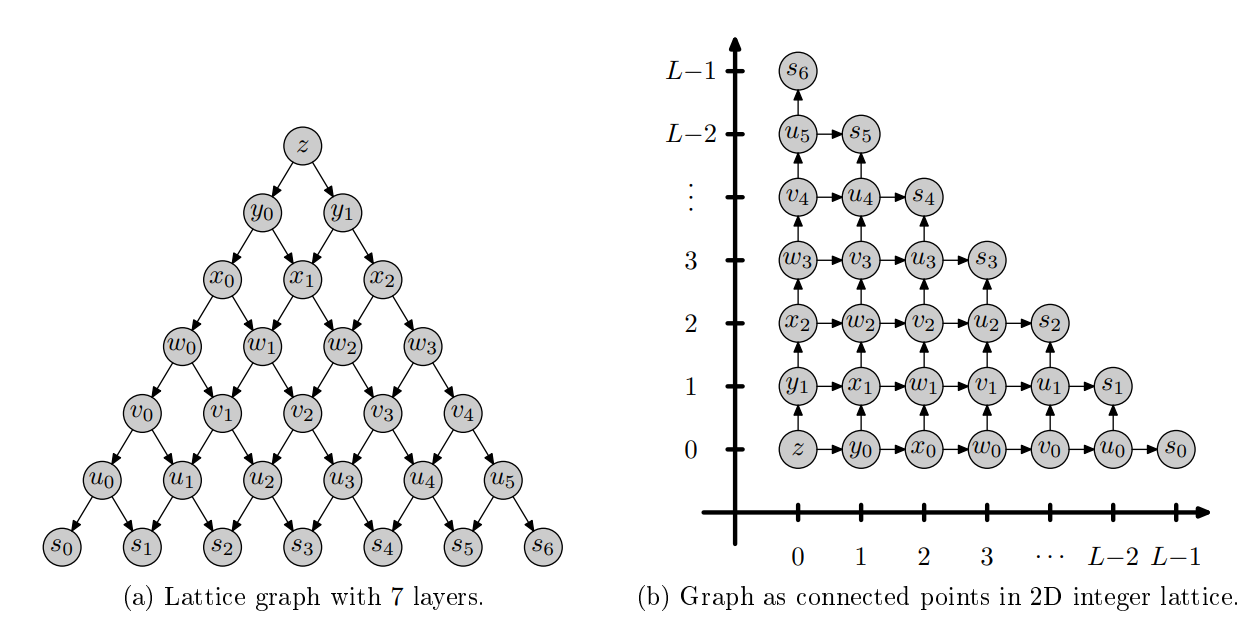
Suppose we start in the unique source vertex on level 0 and walk along edges in the graph, flipping a fair coin at every vertex to decide whether to go left or right, until we reach one of the sinks in the last layer. For instance, in Figure 1a the walk "left-left-right-left-right-right" would visit vertices z, y0, x0, w1, v1, u2, and end in s3.

L-1 S6 L-2 U5 S5 : 14 U4 S4 Yi 3 W3) U3 U3 S3 (To 21 22 2 22 W2 02 (U2 S2 wo (W1 (W2 (W3 1 Y1 21 (W1 U1 U1 S1 VO U2 03 04 0 Yo Xowo (Voluo SO U5 + So Si S2 S3 $4 85 S6 0 1 2 3 L-2 L-1 (b) Graph as connected points in 2D integer lattice. (a) Lattice graph with 7 layers. 3 (100 p) Consider a directed graph that consists of L layers numbered from 0 up to L 1, with i +1 vertices in every layer i numbered from 0 to i, and with outgoing edges from vertex j in layer i to vertices j and j + 1 in layer i + 1. See Figure la for an illustration of this graph with 7 layers. We can agree to call this graph a lattice graph (because it can be obtained from a fragment of the integer lattice in 2 dimensions as shown in Figure 1b, but this is actually completely irrelevant to this problem). Suppose we start in the unique source vertex on level 0 and walk along edges in the graph, flipping a fair coin at every vertex to decide whether to go left or right, until we reach one of the sinks in the last layer. For instance, in Figure la the walk left-left-right-left-right-right" would visit vertices z, yo, 20, W1, V1, U2, and end in 33. 3a (40 p) For every vertex si in the lattice graph in Figure la, calculate the probability that such a walk ends in vertex si. Which vertex is the walk most likely to end up in? L-1 S6 L-2 U5 S5 : 14 U4 S4 Yi 3 W3) U3 U3 S3 (To 21 22 2 22 W2 02 (U2 S2 wo (W1 (W2 (W3 1 Y1 21 (W1 U1 U1 S1 VO U2 03 04 0 Yo Xowo (Voluo SO U5 + So Si S2 S3 $4 85 S6 0 1 2 3 L-2 L-1 (b) Graph as connected points in 2D integer lattice. (a) Lattice graph with 7 layers. 3 (100 p) Consider a directed graph that consists of L layers numbered from 0 up to L 1, with i +1 vertices in every layer i numbered from 0 to i, and with outgoing edges from vertex j in layer i to vertices j and j + 1 in layer i + 1. See Figure la for an illustration of this graph with 7 layers. We can agree to call this graph a lattice graph (because it can be obtained from a fragment of the integer lattice in 2 dimensions as shown in Figure 1b, but this is actually completely irrelevant to this problem). Suppose we start in the unique source vertex on level 0 and walk along edges in the graph, flipping a fair coin at every vertex to decide whether to go left or right, until we reach one of the sinks in the last layer. For instance, in Figure la the walk left-left-right-left-right-right" would visit vertices z, yo, 20, W1, V1, U2, and end in 33. 3a (40 p) For every vertex si in the lattice graph in Figure la, calculate the probability that such a walk ends in vertex si. Which vertex is the walk most likely to end up in