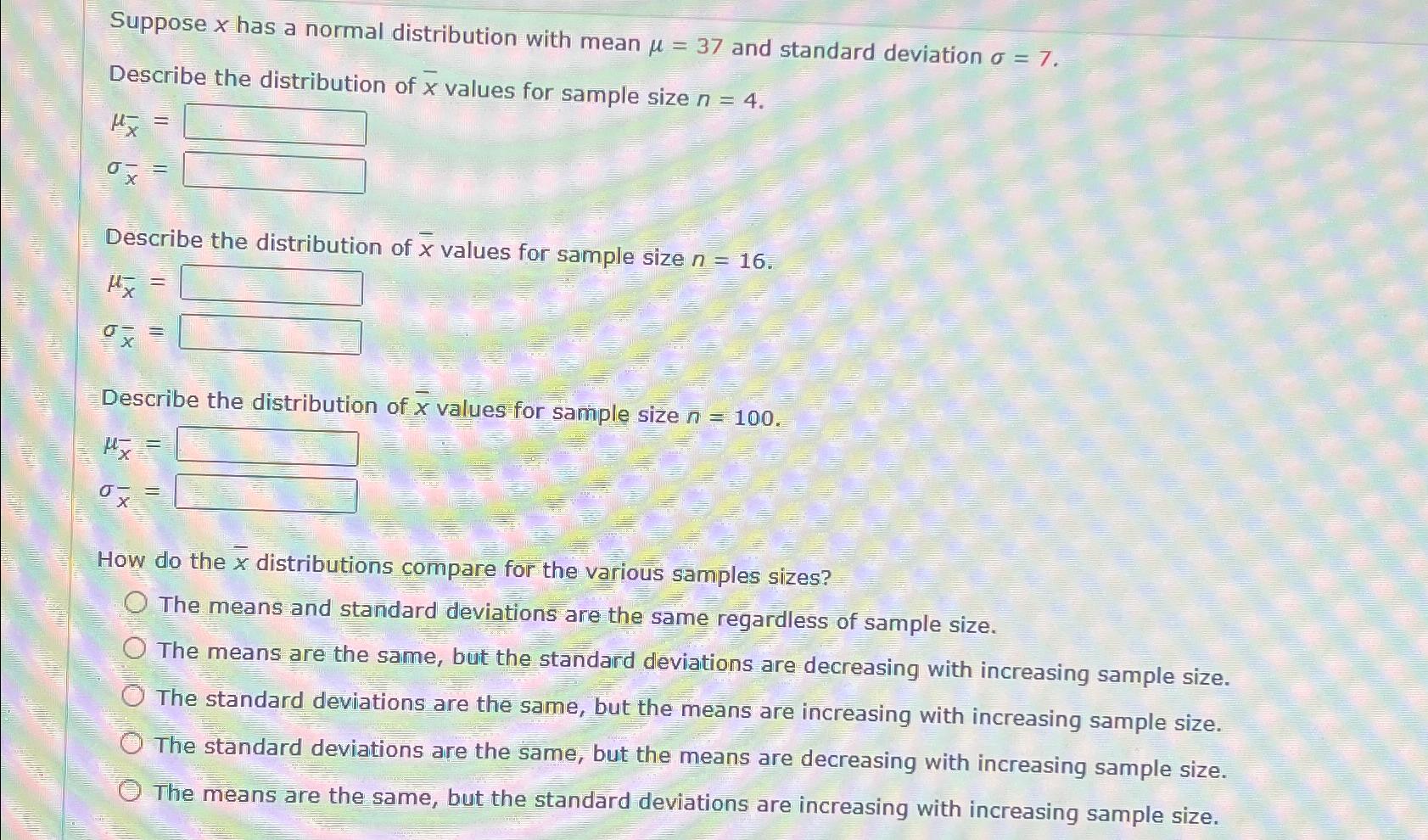
Question: Suppose x has a normal distribution with mean mu =37 and standard deviation sigma =7 . Describe the distribution of bar{x} values for sample size
Suppose
xhas a normal distribution with mean
\\\\mu =37and standard deviation
\\\\sigma =7.\ Describe the distribution of
\\\\bar{x} values for sample size
n=4.\
\\\\mu _(\\\\bar{x} )=\ \\\\sigma _(\\\\bar{x} )=\ Describe the distribution of
\\\\bar{x} values for sample size
n=16.\
\\\\mu _(\\\\bar{x} )=\ \\\\sigma _(\\\\bar{x} )=\ Describe the distribution of
\\\\bar{x} values for sample size
n=100.\
\\\\mu _(\\\\bar{x} )=\ \\\\sigma _(\\\\bar{x} )=\ How do the
\\\\bar{x} distributions compare for the various samples sizes?\ The means and standard deviations are the same regardless of sample size.\ The means are the same, but the standard deviations are decreasing with increasing sample size.\ The standard deviations are the same, but the means are increasing with increasing sample size.\ The standard deviations are the same, but the means are decreasing with increasing sample size.\ The means are the same, but the standard deviations are increasing with increasing sample size.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


