Question: Suppose x is a normally distributed random variable with 11 = 14 and o = 2. Find each of the following probabilities. a. P(x218) b.

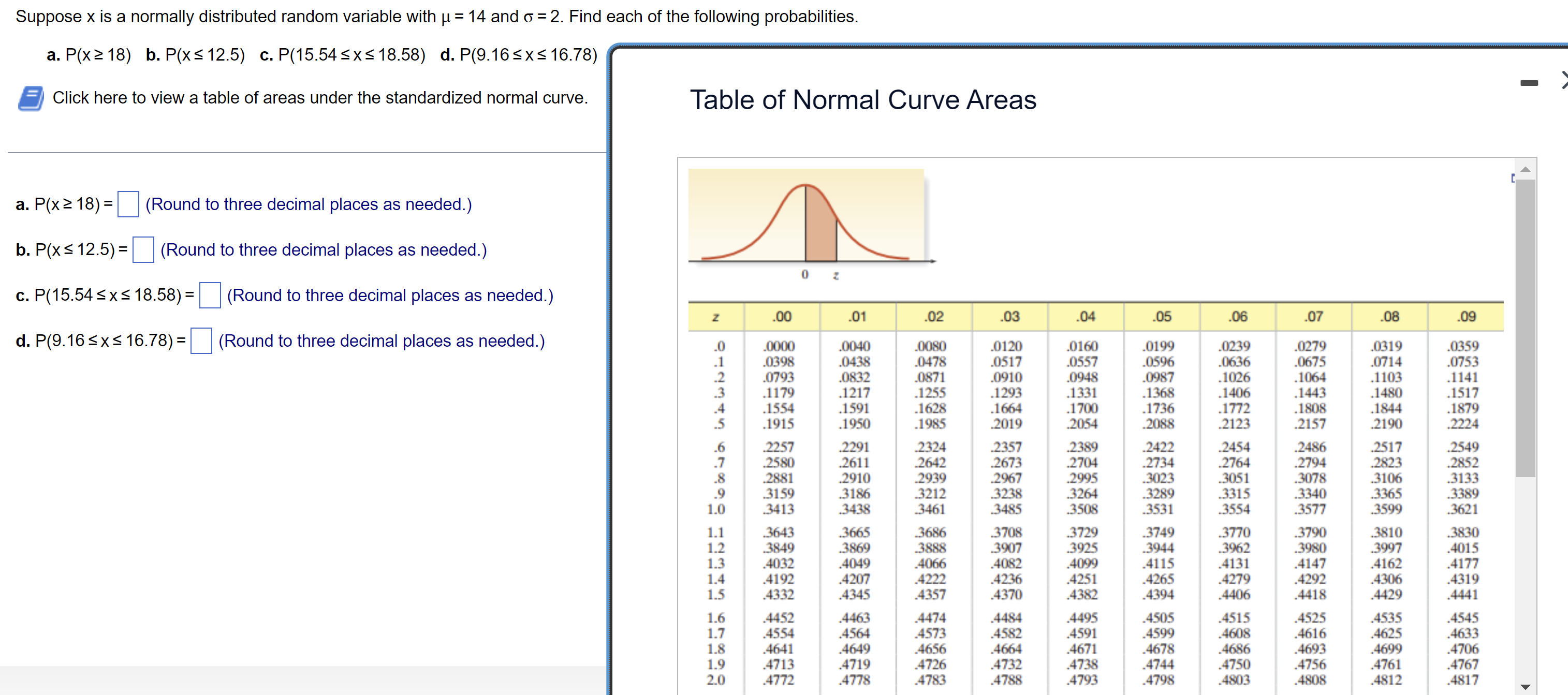
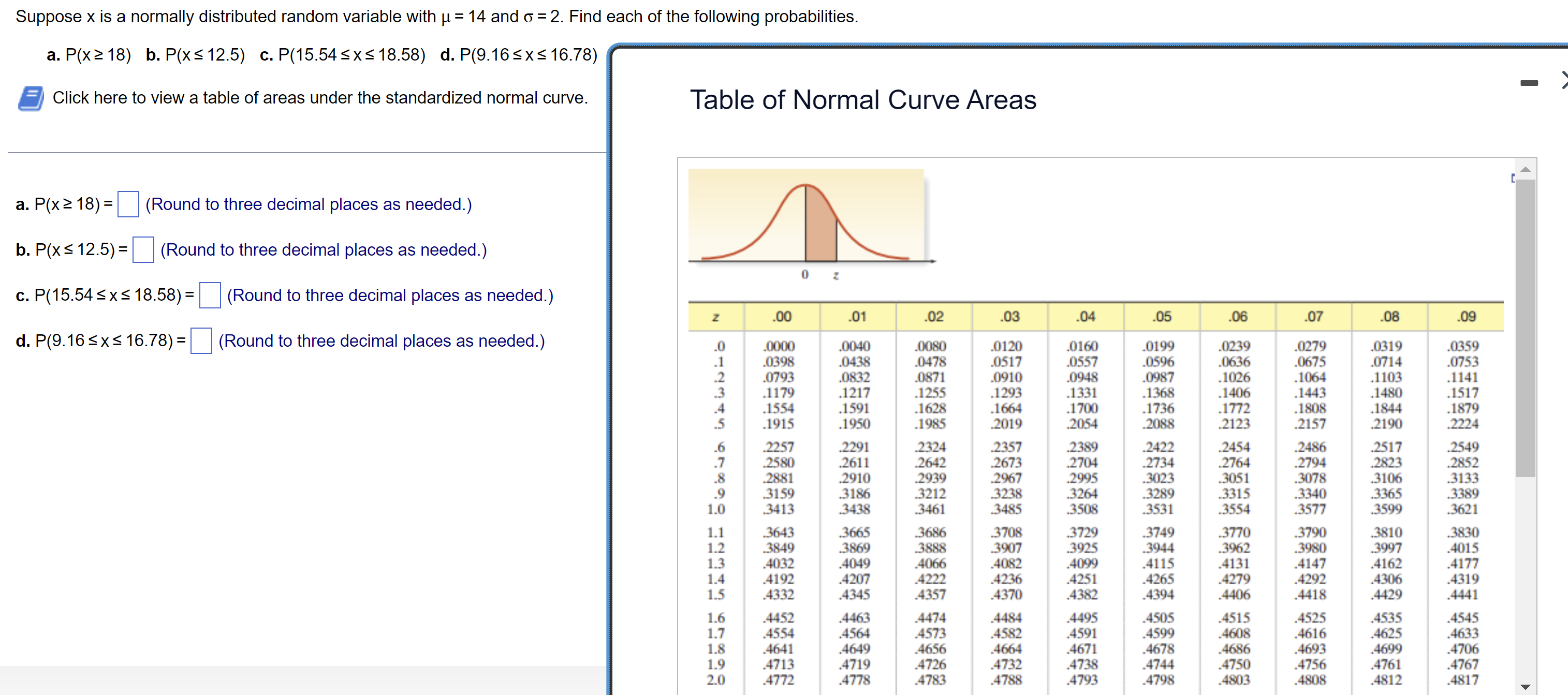
Suppose x is a normally distributed random variable with 11 = 14 and o = 2. Find each of the following probabilities. a. P(x218) b. P(xs'|2.5) c. P(15.54sxs18.58) d.P(9.1esxs16.7s) a Click here to view a table of areas under the standardized normal curve. Tab|e of Norma| Curve Areas A l 1 . a. P(x218)= (Round to three decimal places as needed) 1 b. P(xs12.5)= (Round to three decimal places as needed.) 0 : c. P(15.54sxs18.58)= (Round to three decimal places as needed.) 1 z 00 .01 02 .03 .04 .05 .06 .07 .08 .09 d. P(9.16 S x 5 16.78) = (Round to three decimal places as needed.) _0 .0000 .0040 .0120 .0160 9199 1mg 11379 .0319 1,359 .1 .03911 .0430 .0517 .0557 .0596 .0636 .0675 .0714 .0753 .2 .0793 .0113: .0910 .0941; .0907 .1026 .1064 .1103 .1141 .3 .1179 .1217 .1293 .1331 .1368 .1406 .1443 .14110 .1517 .4 .1554 .1591 .1664 .1700 .1736 .1772 .111011 .1844 .11179 .5 .1915 .1950 2019 .2054 .2088 .2123 .2157 .2190 .2224 .6 2257 .2291 .2357 .2389 .2422 .2454 .2486 .1517 .349 .7 380 .261 1 2673 .2704 .2734 .2764 .2794 .2823 .2852 .8 .2881 .2910 .2967 .2995 .3023 .3051 .3078 .3106 .3133 .9 3159 .3186 338 .3266 .3289 .3315 .3340 .3365 .3389 1 1.0 3413 .3431; 34115 .3531 .3554 .3577 .3599 .3621 1 1.1 31643 .3665 37118 .3749 .3770 .3790 .3810 .3830 1.2 31149 .31169 3907 . .3944 .3962 .3900 .3997 .4015 1 1.3 .4032 .4049 .401L2 .4099 .4115 .4131 .4147 .4162 .4177 1 1.4 .4192 .4207 .4236 .4251 .4265 .4279 .4292 .4306 .4319 1 1.5 .4332 .4345 .4370 .4312 .4394 .4406 .4411; .4429 .4441 1 1.6 .4452 .4463 .4484 .4495 .4505 .4515 .4525 .4535 .4545 1 1.7 .4554 .4564 .451L2 .4591 .4599 .4608 .4616 .4625 .4633 1 1.11 .4641 .4649 .4661 .4671 .4678 .4686 .4693 .4699 .4706 1 1 1.9 .4713 .4719 .4732 .4730 .4744 .4750 .4756 .4761 .4767 l 1 2.0 .4772 .47711 471114 .4793 .4793 .4003 411011 .4812 .4817 1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1. Finding probabilities for standard normal distributions(z)4.85 & 4.872. Finding z-values 4.88, question a, b, d and e only. 4.89, Question a and b only. Finding probabilities for general normal...

Suppose x is a normally distributed random variable with p = 11 and o =2. Find each of the following probabilities. a. P(x 2 12.5) b. P(x =7) c. P(11.48sx= 16.2) d. P(6.04 s x = 14.58) Click here to...

Suppose x is a normally distributed random variable with p = 11 and o = 2. Find each of the following probabilities. a. P(x2 12) b. P(x$9) c. P(12.42 sx 16.3) d. P(6.22 sxs 14.02) Click here to view...

Introduction to Statistics course : here is the question 1-The Standard Normal Distribution note* The solution from this pictures 6.1 | The Standard Normal Distribution The standard normal...

Question 1 (1 point) 1. What is the correct expression for the following sum in summation notation? Xzy4 + X3V6 + X4Ve + XV10 + X6V12 + X7)14 O a) IM X2iVi Ob) Xjy zi Odr Xziyi 1=1 O d) IM- *; y zi...

Mechanical Engineering Department ME 406 Manufacturing and Design First Semester 2017 (Term-171) HOMEWORK # 2 (Engineering Statistics) Assigned by: Dr. Anwar K. Sheikh/Dr Numan Abu Dheir Assigned on...

A lottery ticket has a grand prize of $28 million. The probability of winning the grand prize is .000000023. Determine the expected value of the lottery ticket. (Round your answer to 3 decimal...

Suppose that the present day every day volatilities of asset A and asset B are 1.6% and 2.5%, respectively.The costs of the assets at close of trading the day prior to this had been $20 and $40 and...

IE 0205 Introducion to Decision Analysis Spring 2020 Homework 2 Due: April 9 h , 2020 at 16:00 Answer the following questions. Question 1: Suppose that you have to consider three job offers (defined...

1) The first task is to review some information that might be useful later: a) Write a brief definition of the word "quartile" as we have used it in previous weeks. Be sure to provide a citation:...

Create an augmented matrix for the given linear system. Is this linear system a homogeneous or nonhomogeneous system? x1 + 2x2+2x3 = 2 x1 - x2-x3 = 0 x1 - 3x2-x3 = 0 Perform Gauss Jordan Elimination...

What is the growth rate of output per person in Figure 6.2? What are the growth rates of output per person before and after the changes in the parameter values in Figures 6.3 and 6.4? Figure 6.2...

2 Pulau Penang, Malaysia. Theresa Numn is planning a 3 0 - day vacation on Pulau Penang. Malaysia, one year from now. The present charge for a luxury sute plus meals in Malaysian ringgit ( RM ) is RM...

Harassment. Bernadettes supervisor at Good Drugs asks her if she puts out (offers sex). Bernadette angrily denies that she does and, shortly afterwards, her supervisor has her fired. Bernadette sues...

9. Give an example of how the word because can trigger a cognitive reflex in another party.

7. Give an example of how the authority principle can be used to influence others.

8. Give an example of how the scarcity principle can be used to influence others.