Question: Suppose x is a positive integer with n digits, say x = dd2d3 dn. In other words, di {0, 1, 2, ..., 9} for

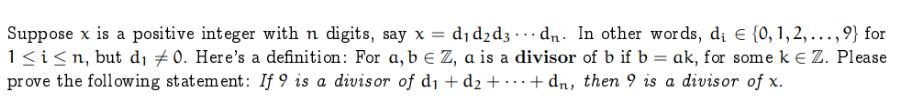
Suppose x is a positive integer with n digits, say x =

Suppose x is a positive integer with n digits, say x = dd2d3 dn. In other words, di {0, 1, 2, ..., 9} for 1 i n, but d #0. Here's a definition: For a, b Z, a is a divisor of b if b = ak, for some k Z. Please prove the following statement: If 9 is a divisor of d + d + + dn, then 9 is a divisor of x.

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Answer Solution 2 is x ddd3 Also p p d 10n1 d we 9 10m 1 and 10 divides 9 9 is div... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Suppose X is a binomial random variable. To approximate P(X

Suppose X is a binomial random variable. To approximate P(3 X 10), compute ____________.

Show if n is a positive integer with n ¥ 2, then (n 3n +2) 4n(n + 1) i2-1 j-2

Write a Python function, add_digits, that sums the digits of a 3-digit integer number. Function add_digits should have one parameter, n, a positive integer with 3 digits, and return the sum of the...

A. Suppose that f(x) is a function that is positive and decreasing. Recall that by the integral test: f: f(:v)da= s f) ft\")- 1 . . . 1 - Recall that e : Z . Suppose that for each positive Integer k,...

=+31. Suppose the random vector X is uniformly distributed on the unit simplex Tn1. Let m be a positive integer with m

if do - a, + a2 - . . . (-1)*a, is divisible by 11. 33. Show that the number 7, 176,825,942, 116,027,211 is divisible by 9 but not divisible by 11. 34. Show that the number 9,897,654,527,609,805 is...

Suppose f(x) is a positive function with a maximum at x*. We can often find maxima and minima of other functions composed with f(x). For each of the functions h(x) = g(f(x)), a. Show that h has a...

Let X = {x1, x2,, xn} and k be a positive integer with k n. Denote by the ratio of the number of k-element permutations among the n elements without repetitions to the number of k-element...

=+13. Suppose q is a positive integer and cm is a sequence of numbers with cm+q = cm for all m. Prove that the series n m=1 cm m converges if and only if q m=1 cm = 0. (Hint: Apply Proposition...

1. Use the diagram below to answer the question. 1600 m X 900 m The area of each square is given in the diagram. What is the value of x + y? A. 30 meters B. 40 meters C. 70 meters D. 120 meters

Which of the following statements are true? -10-8 -6 4 -2 2. 8 10 g(x) O A. Both graphs have exactly one asymptote. O B. Both graphs are exponential functions. O C. Both graphs are logarithmic...

Question 1 6 2 pts The denominator used to compute the allocated budgeted freed manufacturing overhead rate represents levels of factory capacity. They include theoretical, practical, normal, and...

Riots, Suicides and More, blares an internet headline about a FoxConn factory where iPhones and other Apple products are assembled, Apple is not alone in facing supplier scandals. So have Nike,...

For the fireworks shell of Prob. 2 /145, determine the values of r and when the shell reaches an altitude y = 175 ft. Refer to the printed answers for Prob. 2/145 as needed. Data from Prob. 2 /145 A...

The following amortization and interest schedule reflects the issuance of 10-year bonds by Capulet SpA on January 1, 2016, and the subsequent interest payments and charges. The companys year-end is...

Abernathy Corporation was organized on January 1, 2022. It is authorized to issue 10,000 shares of 8%, $50 par value preference shares, and 500,000 shares of no-par ordinary shares with a stated...

The following were selected from among the transactions completed by Essex Company during March of the current year: Mar. 2. Sold merchandise on account to parsley Co., $32,000, terms 1/10, n/30. the...

choose the correct answer During the progressive era, the term scientific management included C) de-skilling: breaking down each complex, skilled task into its component parts. C) increased worker...

Let X (t) = A(t) cos (0t + ), where A(t) is a wide sense stationary random process independent of and let be a random variable distributed uniformly over . Define a related process Y (t) = A (t)...

If we roll two dice and observe the sum, the most common outcome is 7 and occurs with probability 1/ 6. But what if we roll more than 2 dice? (a) Suppose we roll three dice and observe the sum. What...

Suppose a pseudorandom sequence is constructed using the power residue method. If q = 11, find a value of that leads to a sequence with maximum possible period. X k = ax k 1 mod q, k = 1, 2, 3 Find...

Describe Leading Economic Indicators. What are important criticisms of forecasting ability of Leading Economic Indicators?

All nine transactions for Ralston Sports Co. for September 2011, the first month of operations, are recorded in the following T accounts: Prepare a trial balance, listing the accounts in their proper...

Prepare a trial balance, listing the following accounts in proper sequence. The accounts (all normal balances) were taken from the ledger of Sophie Designs Co. on April 30, 2016.