Suppose you are tasked with creating a program to provide the data for a housing market using machine learning methods. The data submitted to you are grouped in the two text files "test.txt" and "training.txt" respectively. You are given skeleton code in the form of two python scripts, "scaling.py" and "regression.py". The idea and importance behind Scaling.py is to improve the convergence of the gradient descent of the linear regression. Simply put in scaling.py you should first calculate the mean of the sample and its standard deviation. Then you take these values and standardize it by subtracting the mean from each value and dividing by their deviation.

After this you are to use the skeleton code of the regression.py script and create a linear regression model that then creates a gradient descent for it. Each method of the skeleton code is merely suggestions and can be altered as long as the end result is a linear regression model that produces the following:

RMSE, Cost and Gradient for the training and test data.

Skeleton Code for the Simple Regression:

train.txt:

3032 525000 2078 230000 2400 87000 2128 180000 1404 183000 1299 135000 1672 117300 2468 233000 1191 165000 1840 199000 3360 310700 1968 152000 1450 136000 2893 360000 1319 134500 1588 144400 2600 410000 2700 169900 3266 379000 1569 149000 3754 550000 1422 147000 1280 154000 2905 223500 1404 141500 1569 140000 1624 167000 2488 279000 1690 215000 2482 271000 2998 329000 3870 375000 2268 242500 3805 475000 2422 384000 1348 175000 3991 375000 1752 168500 3352 439000 1747 265000 1960 250000 3220 300000 3600 399000 1498 145000 3372 385000 2504 210200 2068 195500 2285 320000 2920 312000 3200 290000

test.txt:

5000 415000 1961 178000 2799 315000 1614 150000 3531 355000 1319 136000 2804 460000 2200 282000 912 126000 1800 165400 1768 203500 2596 222000 1822 234000 1634 158000 1422 142500 1092 148000 2420 205000 1569 140000 3787 425000 2844 370000 2760 200000 1746 150000 1422 142500 4190 395000 3130 188000

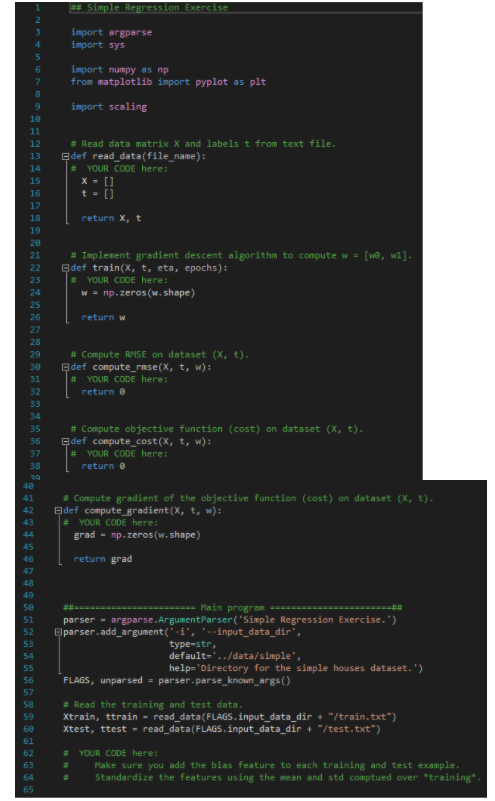
1. Feature Scaling, 10 points] To improve the convergence of gradient descent, it is important that the features are scaled so that they have similar ranges. Implement the scaling to standard normal distribution, using the skeleton code in scaling-py. 2. [Simple Regression, 20 points) Train a simple linear regression model to predict house prices as a function of their floor size, by running gradient descent for 500 epochs with a learning rate of 0.1. Plot J(w) vs. the number of epochs in increments of 10 (i.e. after 0 epochs, 10 epochs, 20 epochs, ...). After training print the parameters and RMSEs and compare with the solution from normal equations. Plot the training using the default blue circles and test examples using lime green triangles. On the same graph also plot the linear approximation. Skeleton code for Scaling.py: import numpy as np # Compute the sample mean and standard deviations for each feature (column) # across the training examples (rows) from the data matrix X. def mean_std(x): np.zeros(X.shape[1]) std = np.ones (X.shape[1]) mean = ## Your code here. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 return mean, std # Standardize the features of the examples in X by subtracting their mean and # dividing by their standard deviation, as provided in the parameters. Eldef standardize(x, mean, std): S = np.zeros(X.shape) ## Your code here. returns ** Simple Regression Exercise a u WNA import argparse import sys import numpy as mp from matplotlib import pyplot as plt import scaling # Read data matrix X and labels t from text file. def read_data(file_name): # YOUR CODE here: x = [] t = 0 8 9 18 11 12 13 14 15 16 17 18 19 28 21 22 23 24 25 26 return xt [we, wa). # Implement gradient descent algorithm to compute w = def train(x, t, eta, epochs): YOUR CODE here: w = np.zeros(w.shape) 17 return w # Compute RMSE on dataset (x, t). Gdef compute_rmse(x, t, w): YOUR CODE here: return @ # 29 38 31 32 33 34 35 36 37 38 # Compute objective function (cost) on dataset (x, t). def compute_cost(x, t, w): YOUR CODE here: return 41 # Compute gradient of the objective function (cost) on dataset (x, t). def compute_gradient(X, t, w): # YOUR CODE here: grad - np.zeros(w.shape) 43 45 46 return grad 48 49 58 51 52 53 54 ---- Main program - parser - argparse. ArgumentParser('Simple Regression Exercise.') Eparser .add_argument(-i', '--input_data_dir", type-str, defaulte'../data/simple', help='Directory for the simple houses dataset.') FLAGS, unparsed = parser.parse_known_args() 56 57 58 59 68 61 62 63 64 65 # Read the training and test data. Xtrain, ttrain - read_data(FLAGS. input_data_dir + "/train.txt") xtest, ttest - read_data(FLAGS. input_data_dir + "/test.txt") # YOUR CODE here: Make sure you add the bias feature to each training and test example. Standardize the features using the mean and std comptued over training* * *