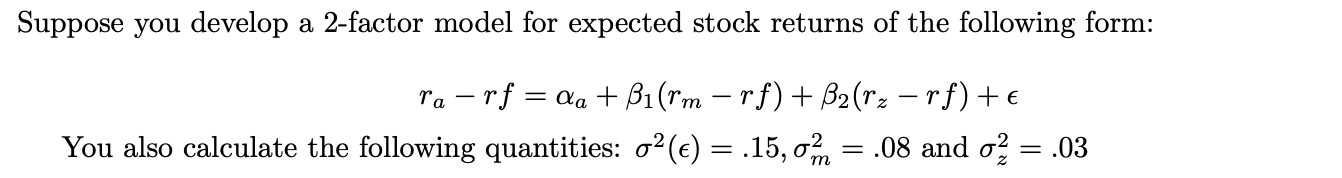
Suppose you develop a 2-factor model for expected stock returns of the following form: ra -rf = 2a + B1(rm rf) + B2 (rz rf) + You also calculate the following quantities: o(e) = .15,0m = .08 and o2 = .03 = Now suppose a fellow analyst believes your model can be improved upon by adding a third factor (r6 -rf). Your boss looks over the new model and notices that the beta to the new factor, B3 is negative. He says that this can't possibly help because the first two factor betas were positive and adding a third factor beta that is negative would lower the predictive power of the model. Is your boss correct or incorrect? Prove your answer. Suppose you develop a 2-factor model for expected stock returns of the following form: ra -rf = 2a + B1(rm rf) + B2 (rz rf) + You also calculate the following quantities: o(e) = .15,0m = .08 and o2 = .03 = Now suppose a fellow analyst believes your model can be improved upon by adding a third factor (r6 -rf). Your boss looks over the new model and notices that the beta to the new factor, B3 is negative. He says that this can't possibly help because the first two factor betas were positive and adding a third factor beta that is negative would lower the predictive power of the model. Is your boss correct or incorrect? Prove your