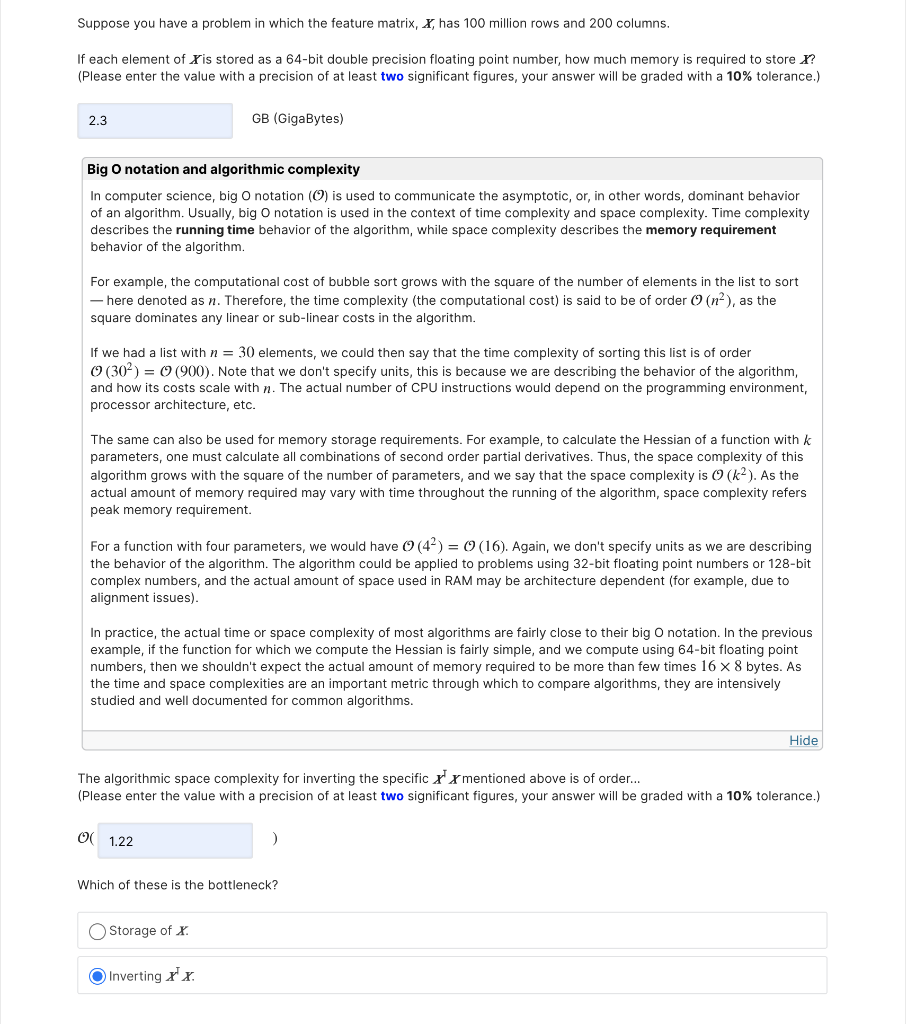
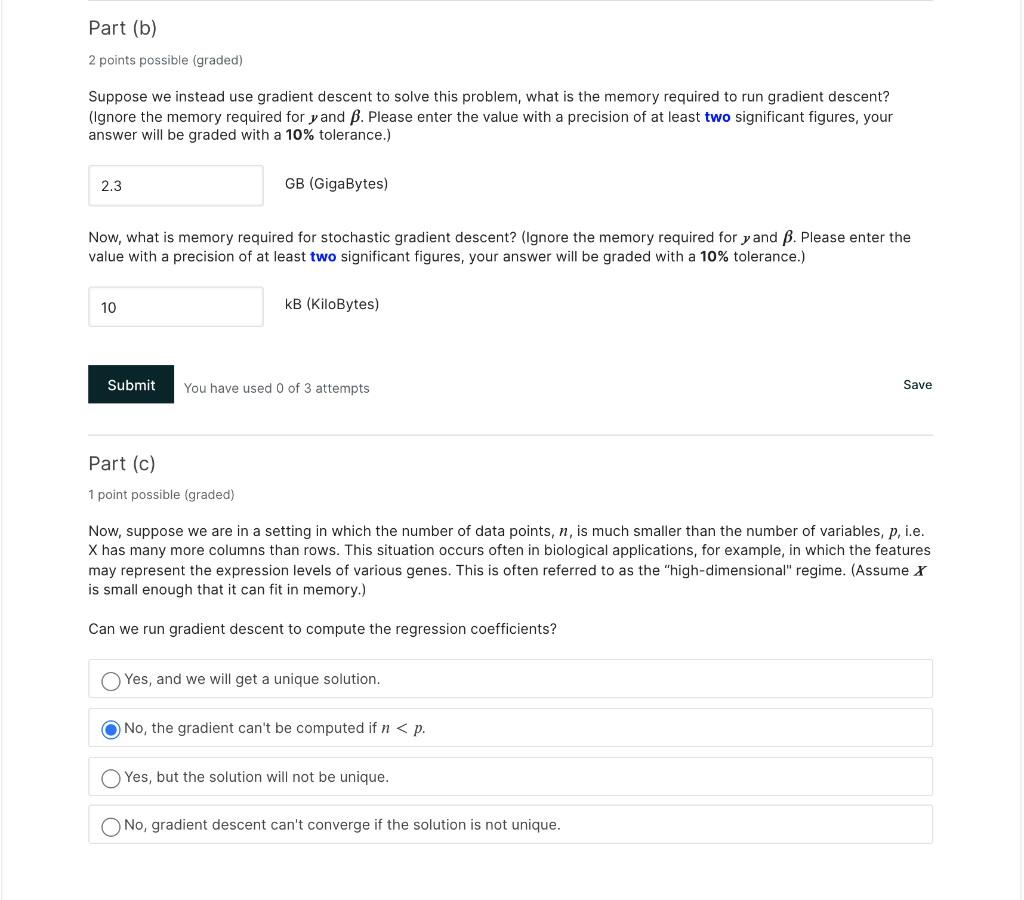
Suppose you have a problem in which the feature matrix, X, has 100 million rows and 200 columns. If each element of X is stored as a 64-bit double precision floating point number, how much memory is required to store ?? (Please enter the value with a precision of at least two significant figures, your answer will be graded with a 10% tolerance.) 2.3 GB (GigaBytes) Big O notation and algorithmic complexity In computer science, big o notation (0) is used to communicate the asymptotic, or, in other words, dominant behavior of an algorithm. Usually, big o notation is used in the context of time complexity and space complexity. Time complexity describes the running time behavior of the algorithm, while space complexity describes the memory requirement behavior of the algorithm. For example, the computational cost of bubble sort grows with the square of the number of elements in the list to sort - here denoted as n. Therefore, the time complexity (the computational cost) is said to be of order () (n), as the square dominates any linear or sub-linear costs in the algorithm. If we had a list with n = 30 elements, we could then say that the time complexity of sorting this list is of order (30%) = (900). Note that we don't specify units, this is because we are describing the behavior of the algorithm, and how its costs scale with n. The actual number of CPU instructions would depend on the programming environment, processor architecture, etc. The same can also be used for memory storage requirements. For example, to calculate the Hessian of a function with k parameters, one must calculate all combinations of second order partial derivatives. Thus, the space complexity of this algorithm grows with the square of the number of parameters, and we say that the space complexity is 0 (k). As the actual amount of memory required may vary with time throughout the running of the algorithm, space complexity refers peak memory requirement. For a function with four parameters, we would have (42) = ((16). Again, we don't specify units as we are describing the behavior of the algorithm. The algorithm could be applied to problems using 32-bit floating point numbers or 128-bit complex numbers, and the actual amount of space used in RAM may be architecture dependent (for example, due to alignment issues). In practice, the actual time or space complexity of most algorithms are fairly close to their big o notation. In the previous example, if the function for which we compute the Hessian is fairly simple, and we compute using 64-bit floating point numbers, then we shouldn't expect the actual amount of memory required to be more than few times 16 x 8 bytes. As the time and space complexities are an important metric through which to compare algorithms, they are intensively studied and well documented for common algorithms. Hide The algorithmic space complexity for inverting the specific x x mentioned above is of order... (Please enter the value with a precision of at least two significant figures, your answer will be graded with a 10% tolerance.) ( 1.22 Which of these is the bottleneck? Storage of x Inverting xx Part (b) 2 points possible (graded) Suppose we instead use gradient descent to solve this problem, what is the memory required to run gradient descent? (Ignore the memory required for y and B. Please enter the value with a precision of at least two significant figures, your answer will be graded with a 10% tolerance.) 2.3 GB (GigaBytes) Now, what is memory required for stochastic gradient descent? (Ignore the memory required for y and B. Please enter the value with a precision of at least two significant figures, your answer will be graded with a 10% tolerance.) 10 kB (kiloBytes) Submit You have used 0 of 3 attempts Save Part (c) 1 point possible (graded) Now, suppose we are in a setting in which the number of data points, n, is much smaller than the number of variables, p, i.e. X has many more columns than rows. This situation occurs often in biological applications, for example, in which the features may represent the expression levels of various genes. This is often referred to as the "high-dimensional" regime. (Assume x is small enough that it can fit in memory.) Can we run gradient descent to compute the regression coefficients? Yes, and we will get a unique solution. No, the gradient can't be computed if n