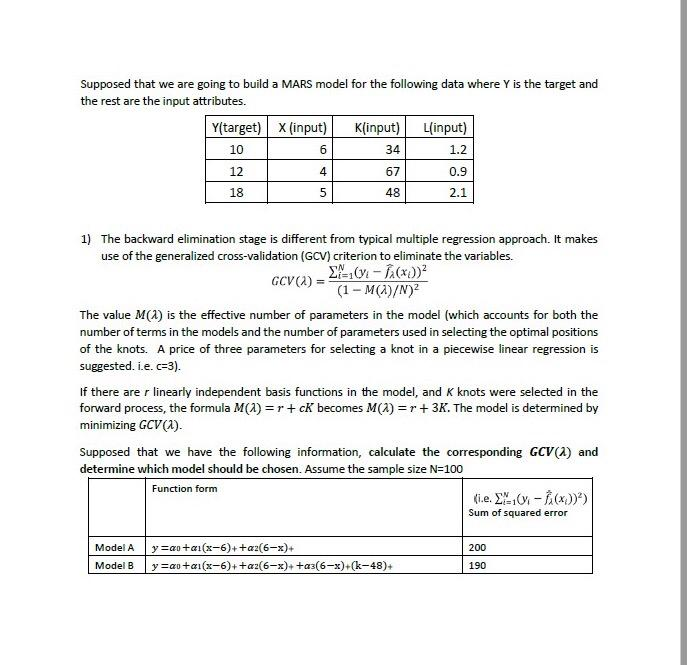
Supposed that we are going to build a MARS model for the following data where Y is the target and the rest are the input attributes. Y(target) x (input) Klinput) L(input) 1 10 6 34 1.2 12 4 67 0.9 - 5 48 2.1 18 1) The backward elimination stage is different from typical multiple regression approach. It makes use of the generalized cross-validation (GCV) criterion to eliminate the variables. GCV) - 9-10.- (x)) ) (1 - M(A)/N)2 The value M(1) is the effective number of parameters in the model (which accounts for both the number of terms in the models and the number of parameters used in selecting the optimal positions of the knots. A price of three parameters for selecting a knot in a piecewise linear regression is suggested. i.e. 3). If there are r linearly independent basis functions in the model, and k knots were selected in the forward process, the formula M(A) = r + cK becomes M(A) = r + 3K. The model is determined by minimizing GCV (A). Supposed that we have the following information, calculate the corresponding GCV (a) and determine which model should be chosen. Assume the sample size N=100 Function form fi.e. - x))) Sum of squared error 200 Model A Model B y y =ao+ai(x-6)++az(6-x)+ =ao+al(x-6)+ +az(6-x)+ +a3(6-x)+(k-48)+ 190 Supposed that we are going to build a MARS model for the following data where Y is the target and the rest are the input attributes. Y(target) x (input) Klinput) L(input) 1 10 6 34 1.2 12 4 67 0.9 - 5 48 2.1 18 1) The backward elimination stage is different from typical multiple regression approach. It makes use of the generalized cross-validation (GCV) criterion to eliminate the variables. GCV) - 9-10.- (x)) ) (1 - M(A)/N)2 The value M(1) is the effective number of parameters in the model (which accounts for both the number of terms in the models and the number of parameters used in selecting the optimal positions of the knots. A price of three parameters for selecting a knot in a piecewise linear regression is suggested. i.e. 3). If there are r linearly independent basis functions in the model, and k knots were selected in the forward process, the formula M(A) = r + cK becomes M(A) = r + 3K. The model is determined by minimizing GCV (A). Supposed that we have the following information, calculate the corresponding GCV (a) and determine which model should be chosen. Assume the sample size N=100 Function form fi.e. - x))) Sum of squared error 200 Model A Model B y y =ao+ai(x-6)++az(6-x)+ =ao+al(x-6)+ +az(6-x)+ +a3(6-x)+(k-48)+ 190