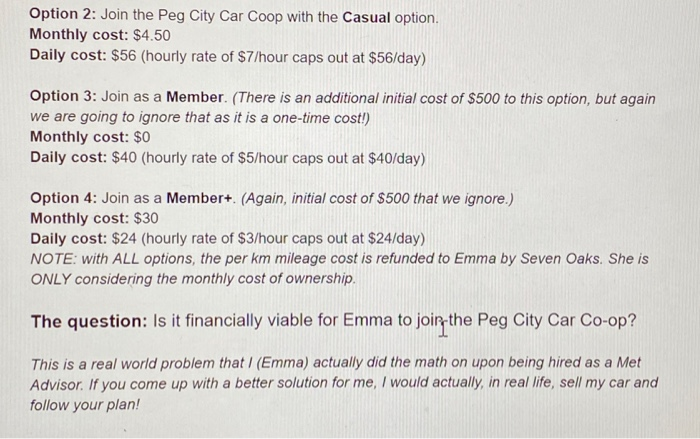
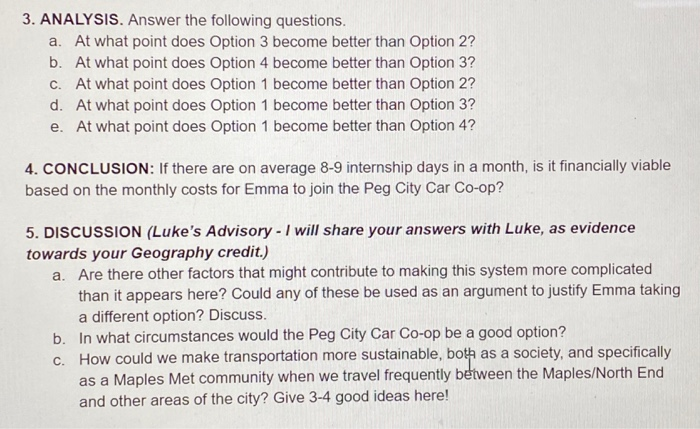
Systems of Equations: A Real World Problem (End-of-Unit Project) The situation (from August 2019): Emma is a person who loves riding her bike. Cycling is good for her mental and physical health, it makes her happy, and it is by far the cheapest transportation option. Plus, it is MUCH better for the planet, with no greenhouse gas emissions! Emma has also recently been hired as an Advisor at the Maples Met School. This is a job that fits very well with most of Emma's values as an educator. The problem: Because Emma's students attend internships on Tuesdays and Thursdays, Emma needs a car in order to fulfil her duties as an Advisor and visit them at their LTI sites. Emma does not want to own a car for personal and ethical reasons. She would prefer to join the Peg City Car Co-op, an organization that places cars around the City of Winnipeg for incidental use by its members. But the amount of time that Emma needs to use the car per month (on average, 8-9 days per month) makes this expensive. Here are her options: Option 1: Own a car. (There is obviously also an initial cost to buying a vehicle, but since this is not a vehicle financing problem, we're just going to ignore that because it is a one-time cost. Assume Emma will buy a cheap car and pay for it outright.) Monthly cost: $200, rounded up from $130.05 (cost of insurance) to account for service/repairs/CAA membership. Daily cost: None. Option 2: Join the Peg City Car Coop with the Casual option. Monthly cost: $4.50 Daily cost: $56 (hourly rate of $7/hour caps out at $56/day) Option 3: Join as a Member. (There is an additional initial cost of $500 to this option, but again we are going to ignore that as it is a one-time cost!) Monthly cost: $0 Daily cost: $40 (hourly rate of $5/hour caps out at $40/day) Option 4: Join as a Member+. (Again, initial cost of $500 that we ignore.) Monthly cost: $30 Daily cost: $24 (hourly rate of $3/hour caps out at $24/day) NOTE: with ALL options, the per km mileage cost is refunded to Emma by Seven Oaks. She is ONLY considering the monthly cost of ownership. The question: Is it financially viable for Emma to joir the Peg City Car Co-op? This is a real world problem that I (Emma) actually did the math on upon being hired as a Met Advisor. If you come up with a better solution for me, I would actually, in real life, sell my car and follow your plan! DIRECTIONS You should submit both a rough draft and a final draft of your solution. The rough draft should be messy and show evidence of you trying different strategies and methods. The final draft should be neat, clear and readable, with your steps and explanations laid out in a logical order. 1. CREATE EQUATIONS. Generate an equation for each of the options, where x (the independent variable) = number of driving days in a month, and y (the dependent variable) = total monthly cost Express each of these equations in slope-intercept (y=mx+b), general (Ax + By + C = 0), AND point-slope form. You should have 4 different equations each expressed 3 ways, so 12 equations in total! 2. SOLVE! For each system of equations, solve graphically AND algebraically. (You may choose substitution or elimination, but please do each one at least once to show you can do both.) a. Option 1 and Option 2 b. Option 1 and Option 3 I C. Option 1 and Option 4 d. Option 2 and Option 3 e. Option 3 and Option 4 3. ANALYSIS. Answer the following questions. a. At what point does Option 3 become better than Option 2? b. At what point does Option 4 become better than Option 3? C. At what point does Option 1 become better than Option 2? d. At what point does Option 1 become better than Option 3? e. At what point does Option 1 become better than Option 4? 4. CONCLUSION: If there are on average 8-9 internship days in a month, is it financially viable based on the monthly costs for Emma to join the Peg City Car Co-op? 5. DISCUSSION (Luke's Advisory - I will share your answers with Luke, as evidence towards your Geography credit.) a. Are there other factors that might contribute to making this system more complicated than it appears here? Could any of these be used as an argument to justify Emma taking a different option? Discuss. b. In what circumstances would the Peg City Car Co-op be a good option? c. How could we make transportation more sustainable, both as a society, and specifically as a Maples Met community when we travel frequently between the Maples/North End and other areas of the city? Give 3-4 good ideas here! RUBRIC ND EM UN- UN+ EX MA Understanding of key concepts and skills Mastery looks like: Answers all questions fully and completely Has checked solutions and corrected own mistakes. Uses a variety of strategies (e.g. graph/substitution/elimination) Accurate use of vocabulary Compelling arguments for real-world problem that are based on mathematical reasoning Clear communication Mastery looks like: Work is neat and readable Language is clear and structured Visuals (e.g. colour-coding in graphs, layout of solution on page) enhance readability ND EM UN- UN+ EX MA I Systems of Equations: A Real World Problem (End-of-Unit Project) The situation (from August 2019): Emma is a person who loves riding her bike. Cycling is good for her mental and physical health, it makes her happy, and it is by far the cheapest transportation option. Plus, it is MUCH better for the planet, with no greenhouse gas emissions! Emma has also recently been hired as an Advisor at the Maples Met School. This is a job that fits very well with most of Emma's values as an educator. The problem: Because Emma's students attend internships on Tuesdays and Thursdays, Emma needs a car in order to fulfil her duties as an Advisor and visit them at their LTI sites. Emma does not want to own a car for personal and ethical reasons. She would prefer to join the Peg City Car Co-op, an organization that places cars around the City of Winnipeg for incidental use by its members. But the amount of time that Emma needs to use the car per month (on average, 8-9 days per month) makes this expensive. Here are her options: Option 1: Own a car. (There is obviously also an initial cost to buying a vehicle, but since this is not a vehicle financing problem, we're just going to ignore that because it is a one-time cost. Assume Emma will buy a cheap car and pay for it outright.) Monthly cost: $200, rounded up from $130.05 (cost of insurance) to account for service/repairs/CAA membership. Daily cost: None. Option 2: Join the Peg City Car Coop with the Casual option. Monthly cost: $4.50 Daily cost: $56 (hourly rate of $7/hour caps out at $56/day) Option 3: Join as a Member. (There is an additional initial cost of $500 to this option, but again we are going to ignore that as it is a one-time cost!) Monthly cost: $0 Daily cost: $40 (hourly rate of $5/hour caps out at $40/day) Option 4: Join as a Member+. (Again, initial cost of $500 that we ignore.) Monthly cost: $30 Daily cost: $24 (hourly rate of $3/hour caps out at $24/day) NOTE: with ALL options, the per km mileage cost is refunded to Emma by Seven Oaks. She is ONLY considering the monthly cost of ownership. The question: Is it financially viable for Emma to joir the Peg City Car Co-op? This is a real world problem that I (Emma) actually did the math on upon being hired as a Met Advisor. If you come up with a better solution for me, I would actually, in real life, sell my car and follow your plan! DIRECTIONS You should submit both a rough draft and a final draft of your solution. The rough draft should be messy and show evidence of you trying different strategies and methods. The final draft should be neat, clear and readable, with your steps and explanations laid out in a logical order. 1. CREATE EQUATIONS. Generate an equation for each of the options, where x (the independent variable) = number of driving days in a month, and y (the dependent variable) = total monthly cost Express each of these equations in slope-intercept (y=mx+b), general (Ax + By + C = 0), AND point-slope form. You should have 4 different equations each expressed 3 ways, so 12 equations in total! 2. SOLVE! For each system of equations, solve graphically AND algebraically. (You may choose substitution or elimination, but please do each one at least once to show you can do both.) a. Option 1 and Option 2 b. Option 1 and Option 3 I C. Option 1 and Option 4 d. Option 2 and Option 3 e. Option 3 and Option 4 3. ANALYSIS. Answer the following questions. a. At what point does Option 3 become better than Option 2? b. At what point does Option 4 become better than Option 3? C. At what point does Option 1 become better than Option 2? d. At what point does Option 1 become better than Option 3? e. At what point does Option 1 become better than Option 4? 4. CONCLUSION: If there are on average 8-9 internship days in a month, is it financially viable based on the monthly costs for Emma to join the Peg City Car Co-op? 5. DISCUSSION (Luke's Advisory - I will share your answers with Luke, as evidence towards your Geography credit.) a. Are there other factors that might contribute to making this system more complicated than it appears here? Could any of these be used as an argument to justify Emma taking a different option? Discuss. b. In what circumstances would the Peg City Car Co-op be a good option? c. How could we make transportation more sustainable, both as a society, and specifically as a Maples Met community when we travel frequently between the Maples/North End and other areas of the city? Give 3-4 good ideas here! RUBRIC ND EM UN- UN+ EX MA Understanding of key concepts and skills Mastery looks like: Answers all questions fully and completely Has checked solutions and corrected own mistakes. Uses a variety of strategies (e.g. graph/substitution/elimination) Accurate use of vocabulary Compelling arguments for real-world problem that are based on mathematical reasoning Clear communication Mastery looks like: Work is neat and readable Language is clear and structured Visuals (e.g. colour-coding in graphs, layout of solution on page) enhance readability ND EM UN- UN+ EX MA