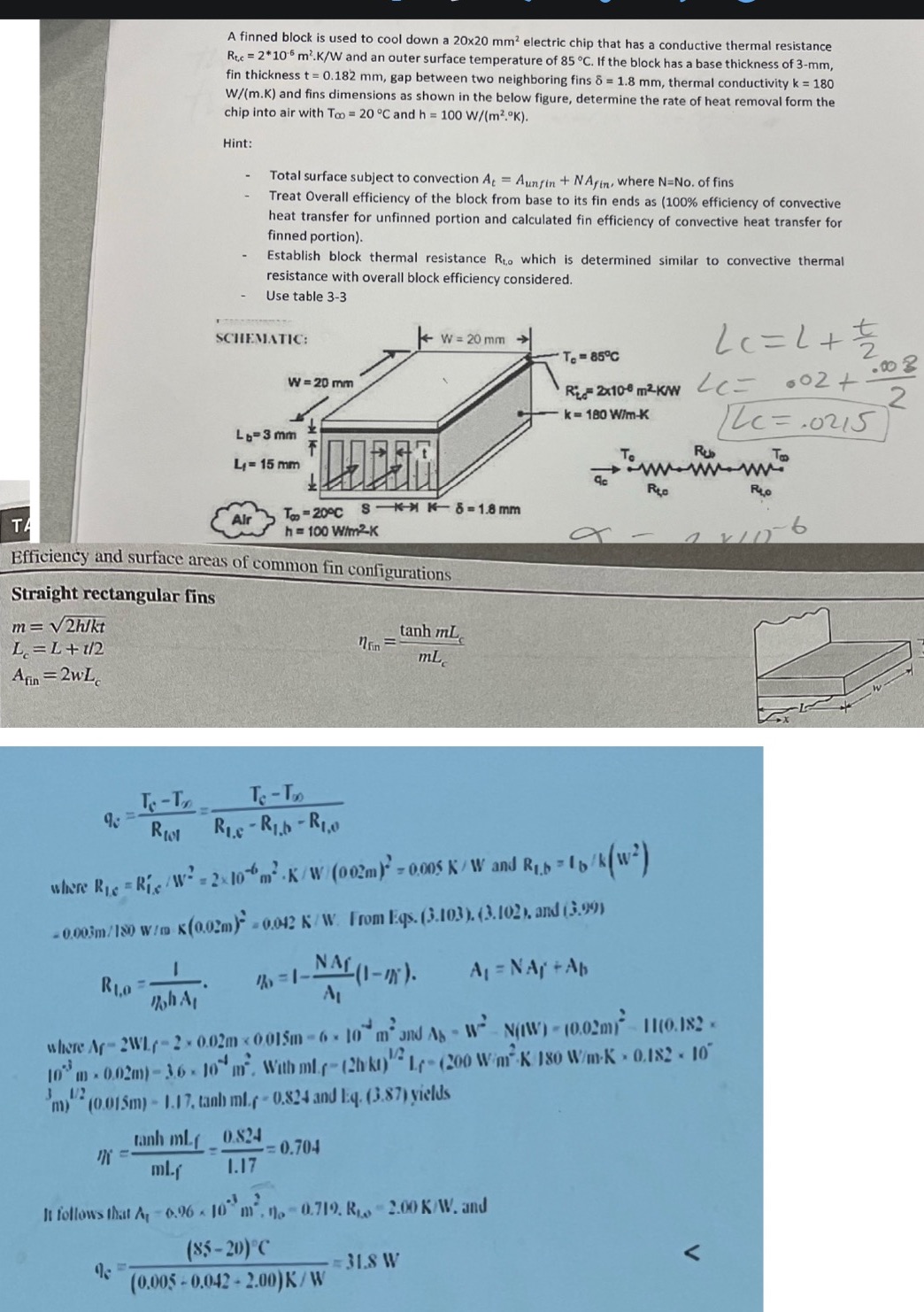
TA A finned block is used to cool down a 20x20 mm electric chip that has a conductive thermal resistance Rtc 2*106 m.K/W and an outer surface temperature of 85 C. If the block has a base thickness of 3-mm, fin thickness t = 0.182 mm, gap between two neighboring fins 8 = 1.8 mm, thermal conductivity k = 180 W/(m.K) and fins dimensions as shown in the below figure, determine the rate of heat removal form the chip into air with Too 20 C and h = 100 W/(m2.K). Hint: Total surface subject to convection At Aunfin + NAfin, where N-No. of fins Treat Overall efficiency of the block from base to its fin ends as (100% efficiency of convective heat transfer for unfinned portion and calculated fin efficiency of convective heat transfer for finned portion). Establish block thermal resistance Rto which is determined similar to convective thermal resistance with overall block efficiency considered. Use table 3-3 SCHEMATIC: W=20 mm Lc = 1 + + T-85C W=20 mm R2x10-6 mK/W k=180 W/m-K Lb 3 mm LC= .02+ c=.0215 .00 2 2 Rub L= 15 mm ac www Tap Ro Air Top-20C h=100 W/m2K SK8=1.8 mm Efficiency and surface areas of common fin configurations Straight rectangular fins m=V2h/kt L = L+ 1/2 Afin = 2wL T-T % 11 Riot Te-T Re-Rib-R1,0 nfin= tanh mL mL 1 b/k (w) where R =Rig/W=210m K/W/(002m) -0.005 K/W and Rb=1b/ -0.003m/180 W/m K(0.02m)=0.042 K/W. From Eqs. (3.103). (3.102), and (3.99) R1,0 =1-- NAL (1-) A = NA +Ab hA AL where Ar-2WL-2-0.02m 0.015m-6-10 m and A-W N(W) (0.02m) 11(0.182- T 12 10 m 0.02m)-3.6-10 m. With ml.-(2hk) L (200 W/mK 180 W/m-K - 0.182 10" 3.4/2 m) (0.015m)-1.17, tanh ml.-0.824 and Eq. (3.87) yields N = tnh ml 0.824 ml.f 1.17 = 0.704 J It follows that A-6.96-10 m. -0.719. R 2.00 K/W. and (85-20)C 4 318 W (0.005-0.042-2.00) K/W