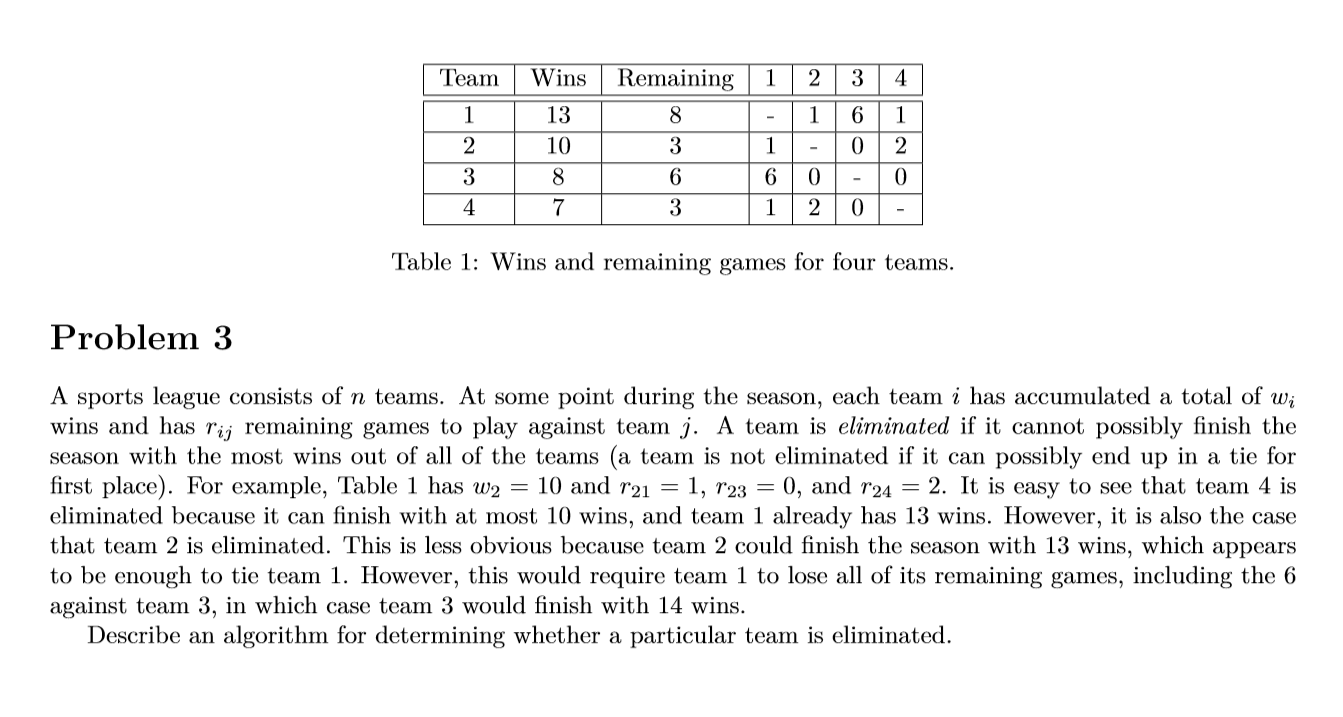
Table 1: Wins and remaining games for four teams. Problem 3 A sports league consists of n teams. At some point during the season, each team 2' has accumulated a total of in, wins and has 73:,- remaining games to play against team 3'. A team is eliminated if it cannot possibly nish the season with the most wins out of all of the teams (a team is not eliminated if it can possibly end up in a tie for rst place). For example, Table 1 has w; = 10 and r21 = 1, r23 = 0, and r24 = 2. It is easy to see that team 4 is eliminated because it can nish with at most 10 wins, and team 1 already has 13 wins. However, it is also the case that team 2 is eliminated. This is less obvious because team 2 could nish the season with 13 wins, which appears to be enough to tie team 1. However, this would require team 1 to lose all of its remaining games, including the 6 against team 3, in which case team 3 would nish with 14 wins. Describe an algorithm for determining whether a particular team is eliminated