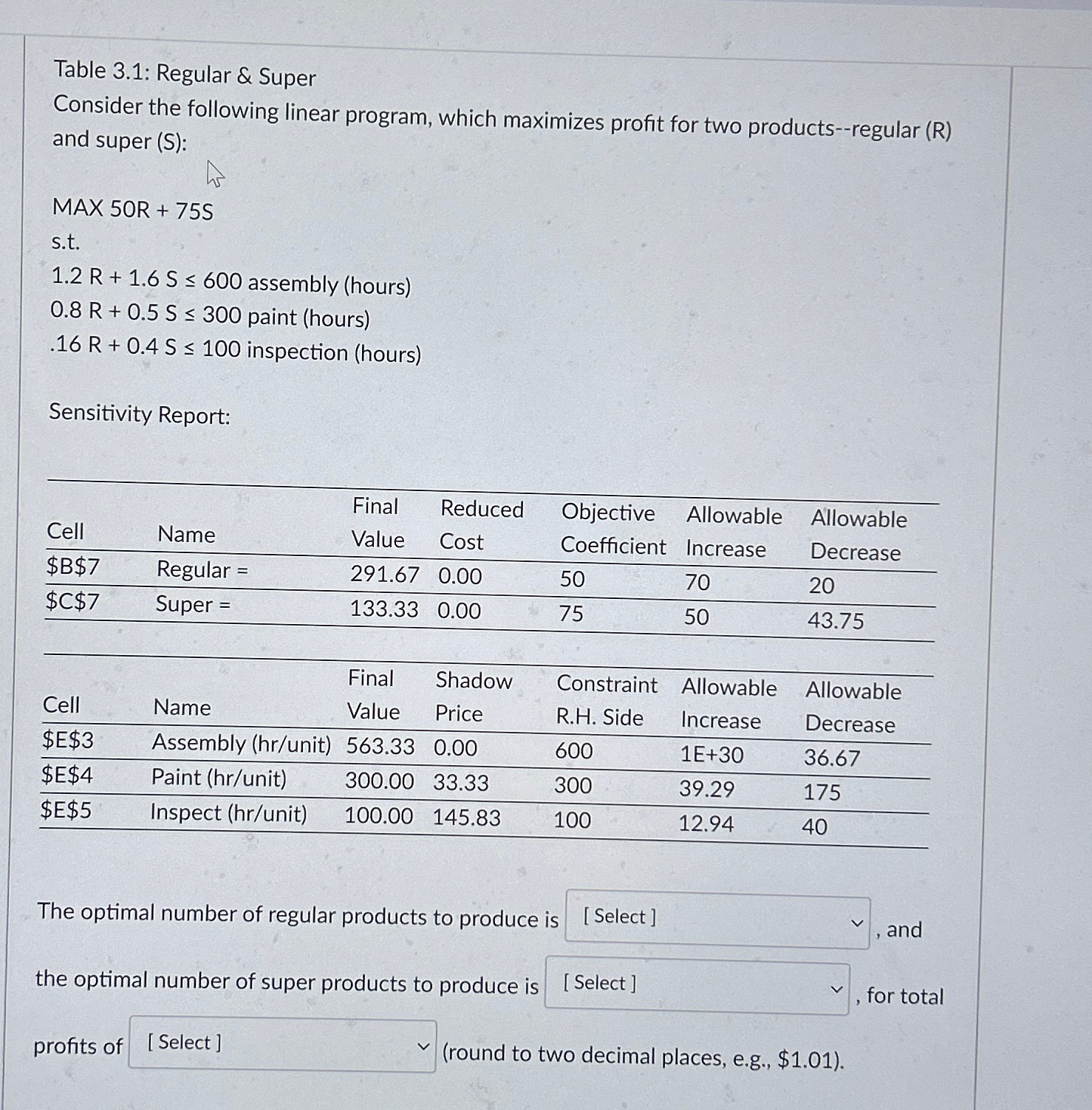
Question: Table 3 . 1 : Regular & Super Consider the following linear program, which maximizes profit for two products - - regular ( R )
Table : Regular & Super
Consider the following linear program, which maximizes profit for two productsregular R and super S:
MAX
assembly
paint
inspection
Sensitivity Report:
tableCellName,tableFinalValuetableReducedCosttableObjectiveCoefficienttableAllowableIncreasetableAllowableDecrease$$Regular $$Super Final,Shadow,Constraint,Allowable,AllowableCellName,Value,Price,RH Side,Increase,Decrease$$Assembly hrunit$$Paint hrunit$E$Inspect hrunit
The optimal number of regular products to produce i and the optimal number of super products to produce is for total profits of round to two decimal places, eg $
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


