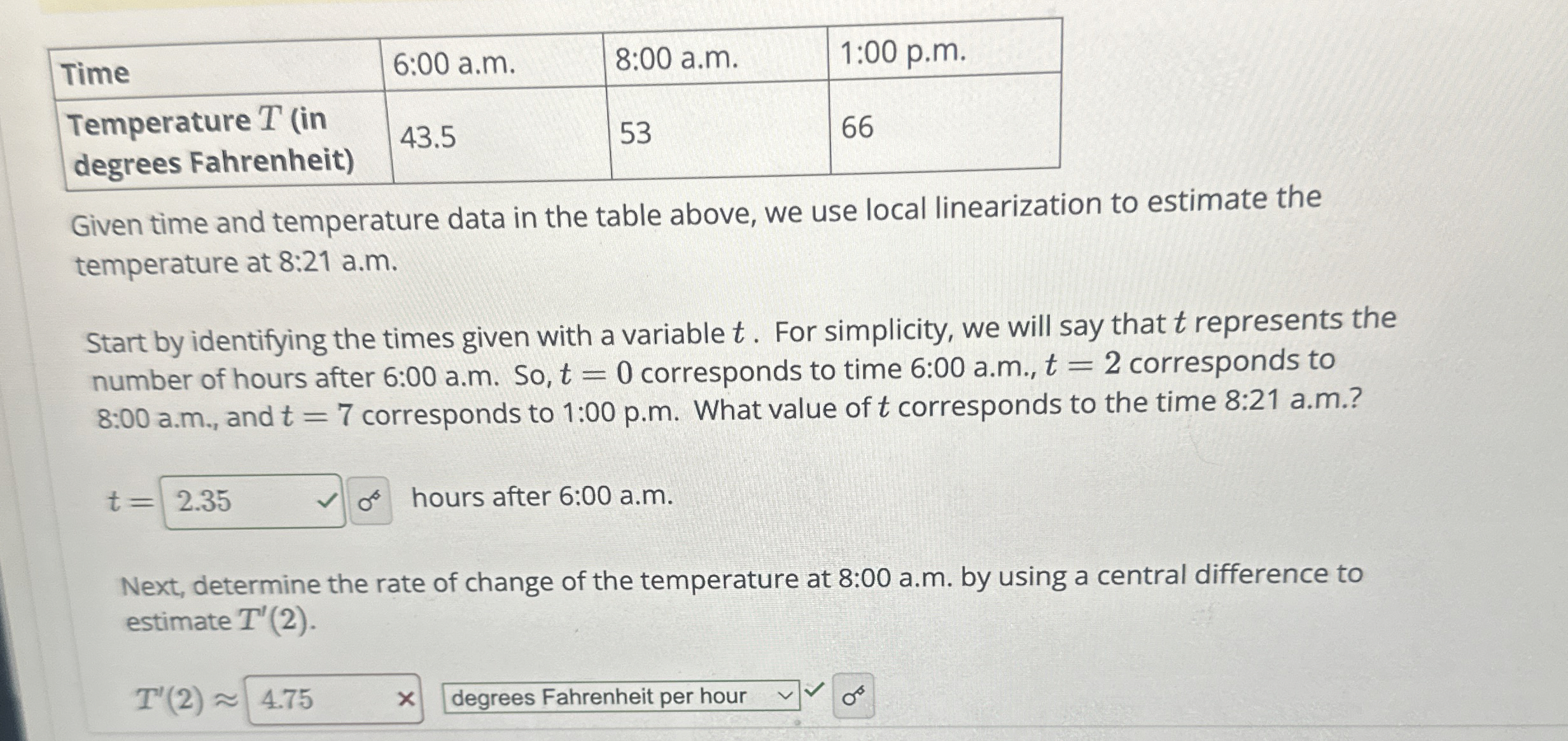
$\backslash$table$[[$Time$,6$:$00$ a$.$m$.,8$:$00$ a$.$m$.,1$:$00$ p$.$m$.],[\backslash$table$[[$Temperature $T($in$],[$degrees Fahrenheit$)]],43\mathrm{.}5,53,66]]$

Given time and temperature data in the table above, we use local linearization to estimate the temperature at $8$:$21$ a$.$m$.$

Start by identifying the times given with a variable $t.$ For simplicity, we will say that $t$ represents the number of hours after $6$:$00$ a$.$m$.$ So$,t=0$ corresponds to time $6$:$00$ a$.$m$.,t=2$ corresponds to $8$:$00$ a$.$m$.,$ and $t=7$ corresponds to $1$:$00$ p$.$m$.$ What value of $t$ corresponds to the time $8$:$21$ a$.$m$.?$

$t=0^6$ hours after $6$:$00$ a$.$m$.$

Next, determine the rate of change of the temperature at $8$:$00$ a$.$m$.$ by using a central difference to estimate $T^{\text{'}}(2).$

$T^{\text{'}}(2)$~~ $$Start by identifying the times given with a variable $t.$ For simplicity, we will say that $t$ represe number of hours after $6$:$00$ a$.$m$.$ So$,t=0$ corresponds to time $6$:$00$ a$.$m$.,t=2$ corresponds $8$:$00$ a$.$m$.,$ and $t=7$ corresponds to $1$:$00$ p$.$m$.$ What value of $t$ corresponds to the time $8$:$21$ a

$t=$ hours after $6$:$00$ a$.$m$.$

Next, determine the rate of change of the temperature at $8$:$00$ a$.$m$.$ by using a central differenc estimate $T^{\text{'}}(2).$

$T^{\text{'}}(2)$~~

$$

$$

Finally, use a local linearization for $T(t)$ at $t=2$ to estimate the temperature at $8$:$21$ a$.$m$.$

Estimated temperature at time $8$:$21$ a$.$m$.$: $$ degrees Fahrenheit