Tail Recursion

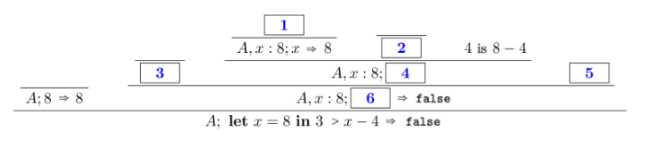
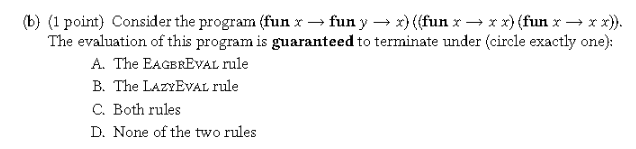
3. (2 points) Consider the integer tree type type tree - Leaf I Node of tree * int * tree The simplest way to calculate the sum of an integer tree is: let rec sum t - match t with Leaf 0 Node (l,v,r)sum(+v+sumr However, this implementation is not tail-recursive. Write a tail recursive function sumtailrec : tree int that sums up the integer values in a tree. (Hint: Use an auxiliary function of type: int tree list int). Operational Semantics 4. (1 point) Derivations Fill in the blanks in the derivation tree for evaluating let x=8 in 3>x4. A;falsefalse(1)A;truetrue(2)A;nn(3)A;xvA(x)=vA;e1>e2vA;e1n1A;e2n2visn1>n2A;ife1thene2elsee3vA;e1trueA;e2v(6e1n1A;e2n2visn1n2A;e1e2vA;ife1thene2elsee3vA;e1falseA;e3vA;letx=e1ine2v2A;e1v1A,x:v1;e2v2(9) Figure 1: Operational Semantics A;88 A; let x=8 Blank 1: Blank 2: Blank 3: Blank 4: Blank 5: Blank 6: 5. (2 points) Operation Semantics Rules (a) (1 point) Consider the operation semantics rules for function calls (or function applications) presented in Lecture 11 or Assignment 4: EAGEREVAL A;12v2A;1(funx)A;2v1A5x:v1;v2 We call this rule EAGBEEVAL because it evaluates the function application argument e2 to a value before evaluating the function body e from e1. Using this evaluation rule, the interpreter can reduce the OCaml program (fun x fun yxy ) (fun c c) ( ( fun aa) (fun bb )) in the following few steps (we omit the environment A for simplicity): (fun x fun yxy ) (fun cc ) (( fun aa)( fun bb )) (fun y( fun cc)y 1) (( fun aa)( fun bb)) (fun y (fun cc ) y 1) (fun bb ) (fun cc)( fun bb)1 (fun bb ) 1 1 It is important to note that function application is left-associative e.g. xyz(xy)z. We now define a new function application evaluation rule called LAzVEvaL as follows: LAZYEVAL A;12v2A;1(funx)A;{2/x}2 Here, e{e2/x} means "the expression after substituting occurrences of x in e with e2 ". The key point is that we defer the evaluation of the functional application argument e2 until it has to be evaluated. This is often referred as "lazy evaluation". Reduce the same OCaml program (fun x fun yxy ) (fun cc ) ((fun a a) (fun bb )) using this new evaluation rule to witness the key difference between EagbeVval and LazYEval. (b) (1 point) Consider the program (fun x fun yx)( fun xxx)( fun xxx)). The evaluation of this program is guaranteed to terminate under (circle exactly one): A. The EAGBREvat rule B. The LazYEvai rule C. Both rules D. None of the two rules