Tansition matrix;

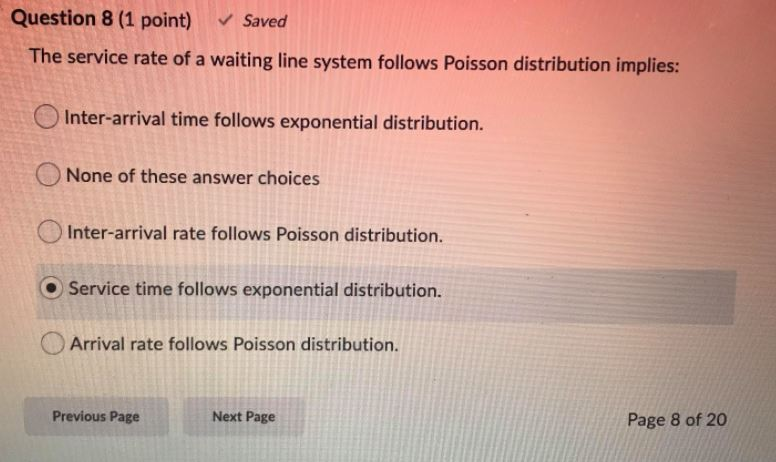
Use the transition diagram in figure a (Model 1) to calculate the probability of the string of states BAB.

Use the transition diagram in figure b (Model 2) to calculate the probability of the string of states CCD.

Use the transition diagram in figure c (Model 3) to calculate the probability of the string of states EEF.

Use the transition diagram in figure d (Model 4) to calculate the probability of the string of states GGG.

An ion channel can be in either open (O) or closed (C) states. If it is open, then it has probability 0.1 of closing in 1 microsecond; if closed, it has probability 0.3 of opening in 1 microsecond. Calculate the probability of the ion channel going through the following sequence of states: COO.

An individual can be either susceptible (S) or infected (I), the probability of infection for a susceptible person is 0.05 per day, and the probability an infected person becoming susceptible is 0.12 per day. Calculate the probability of a person going through the following string of states: SISI.

The genotype of an organism can be either normal (wild type, W) or mutant (M). Each generation, a wild type individual has probability 0.03 of having a mutant offspring, and a mutant has probability 0.005 of having a wild type offspring. Calculate the probability of a string of the following genotypes in successive generations: WWWW.

There are three kinds of vegetation in an ecosystem: grass (G), shrubs (S), and trees (T) . Every year, 25% of grassland plots are converted to shrubs, 20% of shrub plots are converted to trees, 8% of trees are converted to shrubs, and 1% of trees are converted to grass; the other transition probabilities are 0. Calculate the probability of a plot of land have the following succession of vegetation from year to year: GSGG.

The nAChR ion channel can be in one of three states: resting (R), closed with Ach bound (C), and open (O) with transition probabilities (per one microsecond): 0.04 (from R to C), 0.07 (from C to R), 0.12 (from C to O) and 0.02 (from O to C); the other transition probabilities are 0. Calculate the probability of the following string of states: OCCR.

(Challenging) We considered a sequence of Bernoulli trials in chapter 4, for example a string of coin tosses where each time heads and tails come up with probability 0.5. Describe this experiment as a Markov model, draw its transition diagram and write its transition matrix.

(Challenging) Now do the same for a sequence of Bernoulli trials where success has probability 0.9 (and failure has probability 0.1).

(Challenging) Can you formulate a test, based on a transition matrix of a Markov model, to tell whether it's generating a string of independent random variables as opposed to a string of random variables that depend on the previous one?

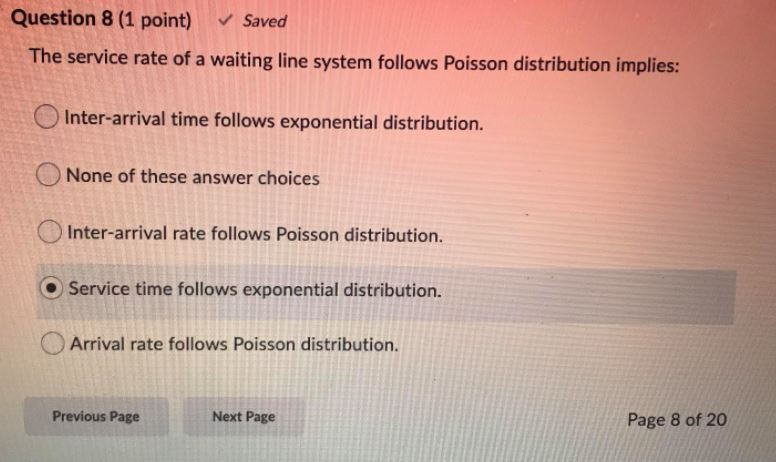
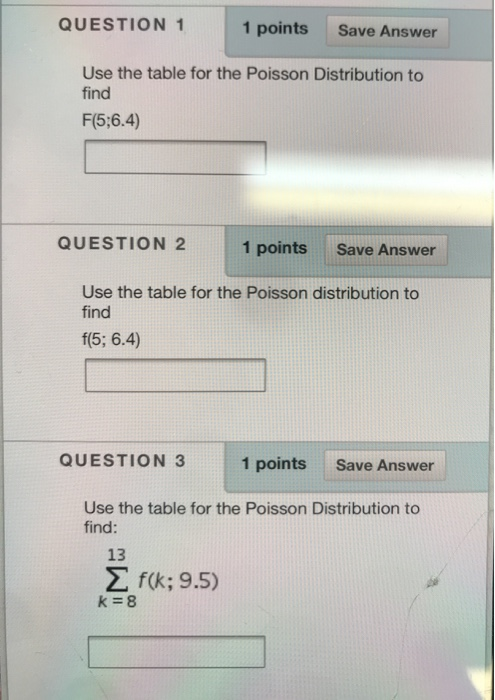
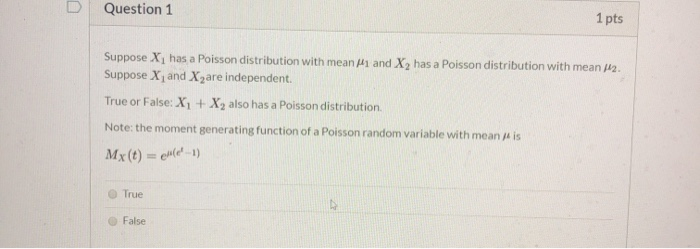
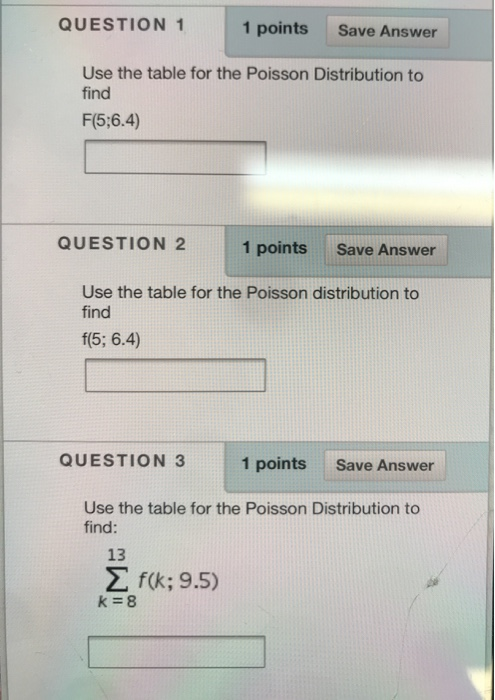
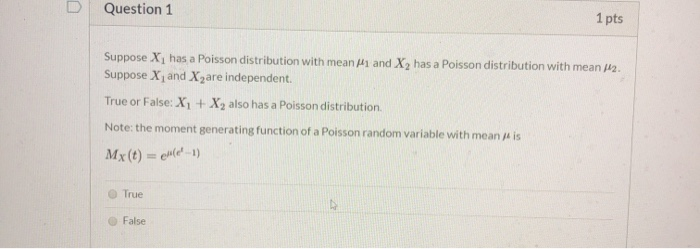
W(n) = The Poisson distribution is given as n! N Wn = 1 (a) Show that it is properly normalized in the sense that n=0 (The sum can be extended to infinity to the excellent approximation, since Wn is neglighibly small when n >N) (b) Use the Poisson distribution to calculate n (c) Use the Poisson distribution to calculate \\bar((\\Delta n)^(2)) = \\bar([n-\\bar(n) ]^(2))Question 8 (1 point) Saved The service rate of a waiting line system follows Poisson distribution implies: Inter-arrival time follows exponential distribution. None of these answer choices Inter-arrival rate follows Poisson distribution. Service time follows exponential distribution. Arrival rate follows Poisson distribution. Previous Page Next Page Page 8 of 20QUESTION 1 1 points Save Answer Use the table for the Poisson Distribution to find F(5;6.4) QUESTION 2 1 points Save Answer Use the table for the Poisson distribution to find f(5; 6.4) QUESTION 3 1 points Save Answer Use the table for the Poisson Distribution to find: 13 E f ( k; 9.5) k =8D Question 1 1 pts Suppose X] has a Poisson distribution with mean #1 and X2 has a Poisson distribution with mean /42. Suppose X, and Xzare independent. True or False: X1 + X2 also has a Poisson distribution. Note: the moment generating function of a Poisson random variable with mean / is Mx (t) = el(e'-1) O True False