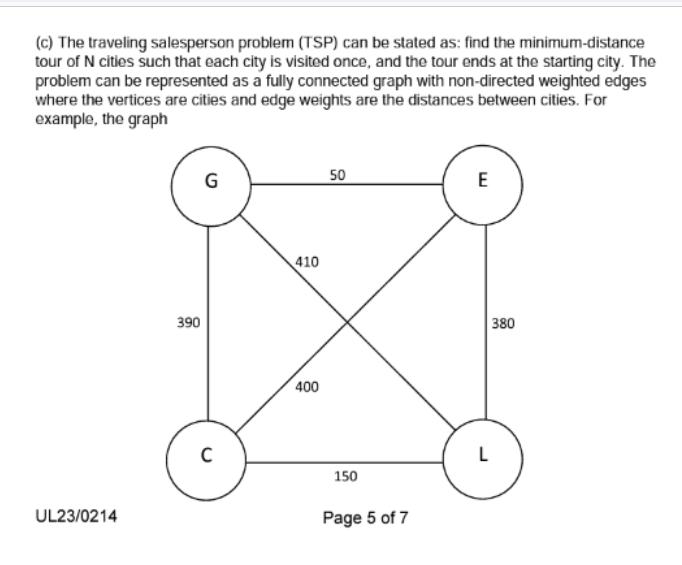
(c) The traveling salesperson problem (TSP) can be stated as: find the minimum-distance tour of N cities such that each city is visited once, and the tour ends at the starting city. The problem can be represented as a fully connected graph with non-directed weighted edges where the vertices are cities and edge weights are the distances between cities. For example, the graph UL23/0214 390 G C 410 400 50 150 Page 5 of 7 E 380 L shows road distances (rounded to the nearest ten miles) between Glasgow, Edinburgh, Cardiff and London. The tour GCELG has distance 390 + 400 +380 + 410 = 1580 miles. (1) Write a pseudocode algorithm that will search for an approximate optimal tour of an N-city TSP. [5 marks] (ii) Consider an algorithm that finds an optimum tour by exhaustive search. What is the time-complexity of this algorithm? [5 marks] (iii) With regard to your answer to (ii) above, and by comparison to the time complexities of algorithms you have studied in this module, what are the prospects for discovering a polynomial time solution to the TSP? [5 marks]