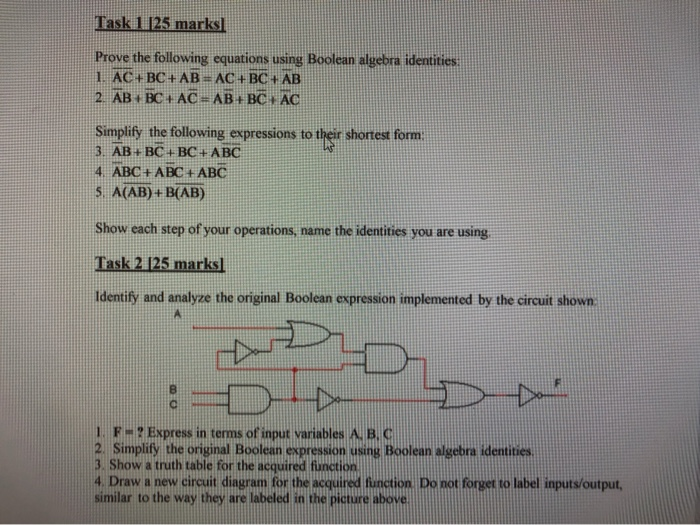
Task 4 [30 marks Make a sequential counter that can loop through composite (ie, not prime) 4-bit numbers (use ABCD format) at each clock pulse. You should rely on D-flip-flops to represent each bit of a current counter state. Draw state diagram, construct present-next state table, and use K-maps for each bit to acquire functions for all D-flip-flop inputs. When your simplified functions are ready. draw a circuit diagram as implementation of the described counter Task 1 125 marksl Prove the following equations using Boolean algebra identities 1. AC+ BC + AB = AC + BC + AB 2. AB + BC + AC = AB+BC AC Simplify the following expressions to their shortest form: 3. AB+ BC + BC + ABC 4. ABC + ABC + ABC 5. A(AB)+B(AB) Show each step of your operations, name the identities you are using Task 2 [25 marks) Identify and analyze the original Boolean expression implemented by the circuit shown een - Det 1. F ? Express in terms of input variables ABC 2. Simplify the original Boolean expression using Boolean algebra identities 3. Show a truth table for the 4. Draw a new circuit diagram for the acquired function. Do not forget to label inputs/output, similar to the way they are labeled in the picture above Task 4 [30 marks Make a sequential counter that can loop through composite (ie, not prime) 4-bit numbers (use ABCD format) at each clock pulse. You should rely on D-flip-flops to represent each bit of a current counter state. Draw state diagram, construct present-next state table, and use K-maps for each bit to acquire functions for all D-flip-flop inputs. When your simplified functions are ready. draw a circuit diagram as implementation of the described counter Task 1 125 marksl Prove the following equations using Boolean algebra identities 1. AC+ BC + AB = AC + BC + AB 2. AB + BC + AC = AB+BC AC Simplify the following expressions to their shortest form: 3. AB+ BC + BC + ABC 4. ABC + ABC + ABC 5. A(AB)+B(AB) Show each step of your operations, name the identities you are using Task 2 [25 marks) Identify and analyze the original Boolean expression implemented by the circuit shown een - Det 1. F ? Express in terms of input variables ABC 2. Simplify the original Boolean expression using Boolean algebra identities 3. Show a truth table for the 4. Draw a new circuit diagram for the acquired function. Do not forget to label inputs/output, similar to the way they are labeled in the picture above