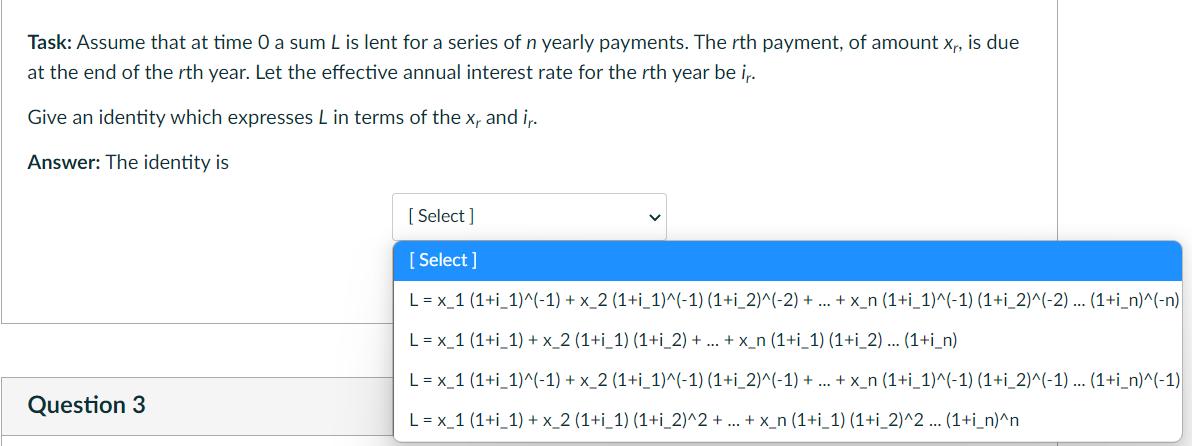
Task: Assume that at time 0 a sum L is lent for a series of n yearly payments. The rth payment, of amount x, is due at the end of the rth year. Let the effective annual interest rate for the rth year be i,. Give an identity which expresses L in terms of the x, and i,. Answer: The identity is [ Select ] [ Select ] L = x_1 (1+i_1)^(-1) + x_2 (1+i_1)^(-1) (1+i_2)^(-2) + ... + x_n (1+i_1)^(-1) (1+i_2)^(-2) ... (1+i_n)^(-n) L = x_1 (1+i_1) + x_2 (1+i_1) (1+i_2) + .. + x_n (1+i_1) (1+i_2)... (1+i_n) L = x_1 (1+i_1)^(-1) + x_2 (1+i_1)^(-1) (1+i_2)^(-1) + . + x_n (1+i_1)^(-1) (1+i_2)^(-1) ... (1+i_n)^(-1) Question 3 L = x_1 (1+i_1) + x_2 (1+i_1) (1+i_2)^2 + ... + x_n (1+i_1) (1+i_2)^2 ... (1+i_n)^n