Question: Task Let f: B(0) R be a function with the property that the partial derivatives of f exist at all points af in B(0).

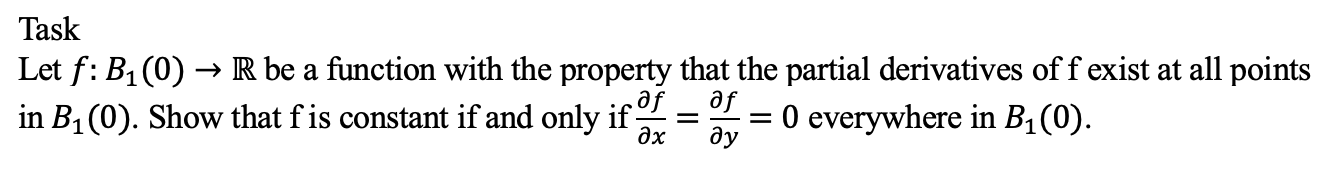
Task Let f: B(0) R be a function with the property that

Task Let f: B(0) R be a function with the property that the partial derivatives of f exist at all points af in B(0). Show that f is constant if and only if of = = 0 everywhere in B(0).

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Fact Pattern: A medium-sized municipality provides 8.5 billion gallons of water per year for 31,000 customers. The water meters are replaced at least every 5 years to ensure accurate billing. The...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

Problem 1. Let r : [0, 1] R n be a differentiable vector function. Assume that kr(t)k is constant on [0, 1]. Show that r 0 (t) is perpendicular to r(t) for every t [0, 1]. Problem 2. Let f : R n R be...

Hi tutor. Kindly help me solve these I1 Exercise 2. Let f: R" + R be a real-valued function on R", and Xo = E R a In point. (a) If f is differentiable at Xo, explain what it means to say that the...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

All questions. 05:50:42 VA; 25% ' ASSIGNMENTNM1.pdf IQ 0+ Numerical Methods-Assignment-l Mathematical Prelimanaries, Taylor's Theorem, Order of Convergence (1) Let L be a real number and let {an} be...

Calculus 3 (Math-UA-123) Fall 2016 Homework 5 Due: Thursday, October 20 at the start of class Please give complete, well-written solutions to the following exercises. 1. The figure on the left shows...

Provide a brief explanation or calculation to justify your answer: (a) Consider the contour plot for f(x,y) shown below. Use the contour plot to determine the sign y 13 please include all steps or i...

In BE2-2, Boeings current assets consisted primarily of cash and short-term investments of $9.3 billion, accounts receivable of $5.7 billion, inventory of $9.6 billion, and miscellaneous current...

Consider an investor who is looking into the performance of a particular portfolio. She found that the historical estimates of the mean and variance of the portfolio's monthly return are 0.95% and...

Joe owns a traditional IRA and names his wife, Holly, as the primary beneficiary. His son, Will, is the contingent beneficiary. If Joe dies, but both Holly and Will are living, which of the following...

What is the primary purpose of analytical procedures performed during the planning stages of the audit? Please identify the warning signs that were revealed about the inventory balance during...

Read the case study Cirque du Soleil Case Analysis and write Summary of Background and Facts

A shaft carries five masses A, B, C, D and E which revolve at the same radius in planes which are equidistant from one another. The magnitude of the masses in planes A, C and D are 50 kg, 40 kg and...

A variable force of 5x-2 pounds moves an object along a straight line when it is x feet from the origin. Calculate the work done in moving the object from x= 1 ft to x = 10 ft.

Computer algebra systems have commands that differentiate functions, but the form of the answer may not be convenient and so further commands may be necessary to simplify the answer. (a) Use a CAS to...

If Where is a continuous function, find f(4). f(t) dt. xsin TX =

=+Assuming the GMAT scores are nearly Normal with N(500,100),

=+The company president vetoes that plan, saying the company should give away less free cereal, not more. Her goal is to set the machine no higher than 16.2 oz and still have only 4% underweight...

=+1 Your Accounting teacher has announced that the lower of your two tests will be dropped. You got a 90 on test 1 and an 80 on test 2. Youre all set to drop the 80 until she announces that she...