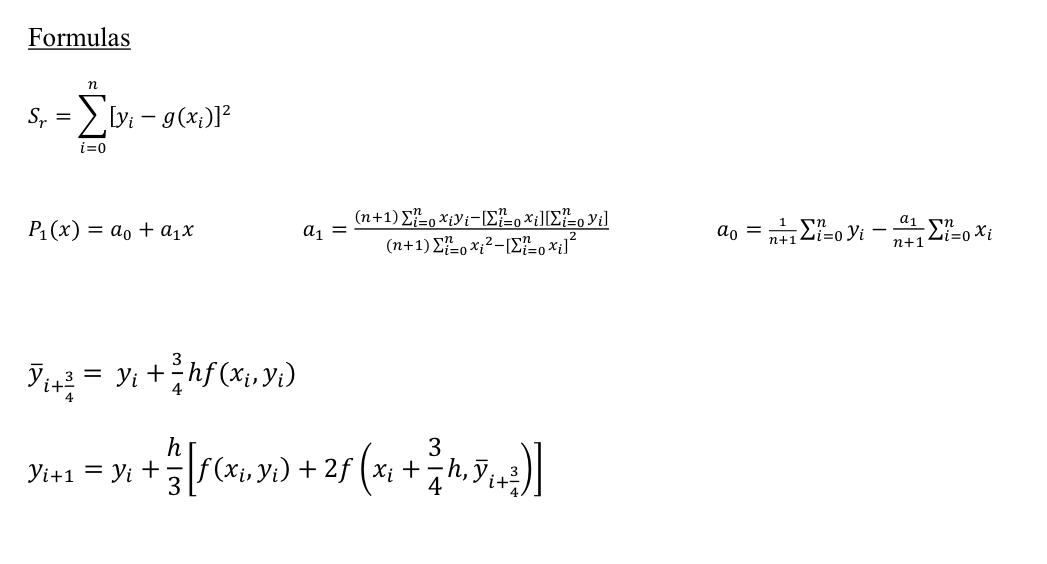
Taylo Formulas Vm+1 = Avm ||Avm|| B = A I B (A 2)(A-1) h h y(xo + h) = y(x0) + hy' (xo) + "(x) + 3y" (x0) + ... RR h Yi+1 = y +[k + 2k2+2k3 + k4] k = f (xi, yi) h 1 k = f (x + y +hk) h k3 = f(x1+ y+hk) k4= f(x+h, y + hk3) Forward 22 Buonund 22 Central 22 22 ax Ui+1,j - ui,j Ax Ui,j-ui-1,j Ax Ui+1,j - 2Ax - U-1,j ui-1,j 2ui,jui+1,j (Ax) Formulas n S = [y = g(x)] i=0 P(x) = a + ax a = V = y +hf(x, y) h (n+1) {=oXiVi=[?=o xt][?=oVi] (n+1) x2 -[=oxi] 3 Yi+1 = Yi + + } } [ f (x, y ) + 2 f ( x 2 + 3 / h, y + ) ] ao = - a1 n+1 2) In the absence of atmospheric drag, the velocity v during the vertical ascent of a rocket may be calculated by solving the differential equation == dv dt = mo-met subject to the initial condition v(0) = 0. Here t is time, me is the rate of fuel and oxidizer consumption, c is the velocity of the exhaust gases, mo is the mass of the fully-fueled rocket at launch, and g is the gravitational acceleration 9.807 m/s. For a Falcon 9 rocket, me = 2100 kg/s, c 3000 m/s and mo=525,000 kg. Calculate the velocity (in meters/sec) of the Falcon 9 rocket one second after liftoff a) By analytically solving the differential equation. b) By calculating the first 3 nonzero terms using Taylor's expansion approach. c) By using the classical fourth-order Runge-Kutta method with a step-size of 1 sec.