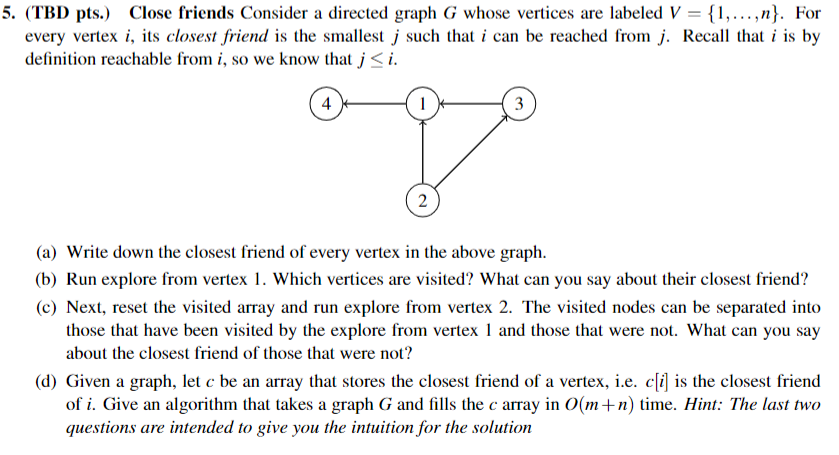
(TBD pts.) Close friends Consider a directed graph G whose vertices are labeled V={1,,n}. For every vertex i, its closest friend is the smallest j such that i can be reached from j. Recall that i is by definition reachable from i, so we know that ji. (a) Write down the closest friend of every vertex in the above graph. (b) Run explore from vertex 1. Which vertices are visited? What can you say about their closest friend? (c) Next, reset the visited array and run explore from vertex 2. The visited nodes can be separated into those that have been visited by the explore from vertex 1 and those that were not. What can you say about the closest friend of those that were not? (d) Given a graph, let c be an array that stores the closest friend of a vertex, i.e. c[i] is the closest friend of i. Give an algorithm that takes a graph G and fills the c array in O(m+n) time. Hint: The last two questions are intended to give you the intuition for the solution