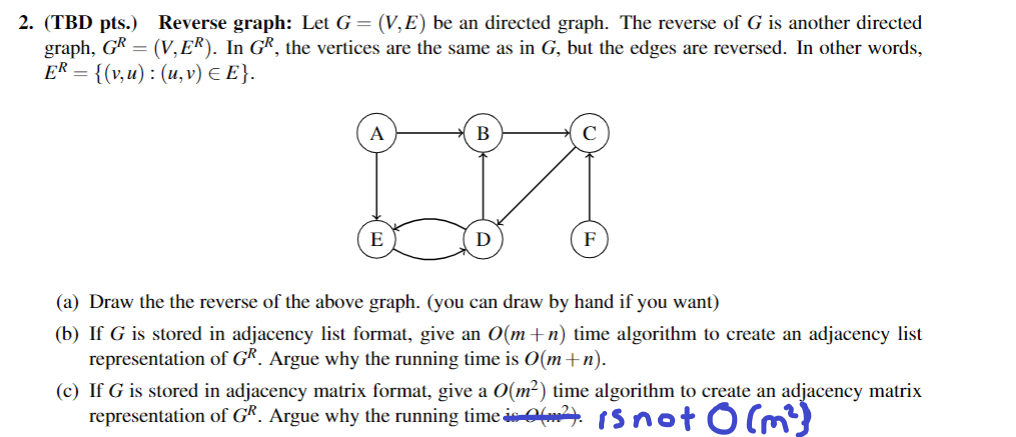
(TBD pts.) Reverse graph: Let G=(V,E) be an directed graph. The reverse of G is another directed graph, GR=(V,ER). In GR, the vertices are the same as in G, but the edges are reversed. In other words, ER={(v,u):(u,v)E}. (a) Draw the the reverse of the above graph. (you can draw by hand if you want) (b) If G is stored in adjacency list format, give an O(m+n) time algorithm to create an adjacency list representation of GR. Argue why the running time is O(m+n). (c) If G is stored in adjacency matrix format, give a O(m2) time algorithm to create an adjacency matrix representation of GR. Argue why the running time i(m2) is n0+0(m2)