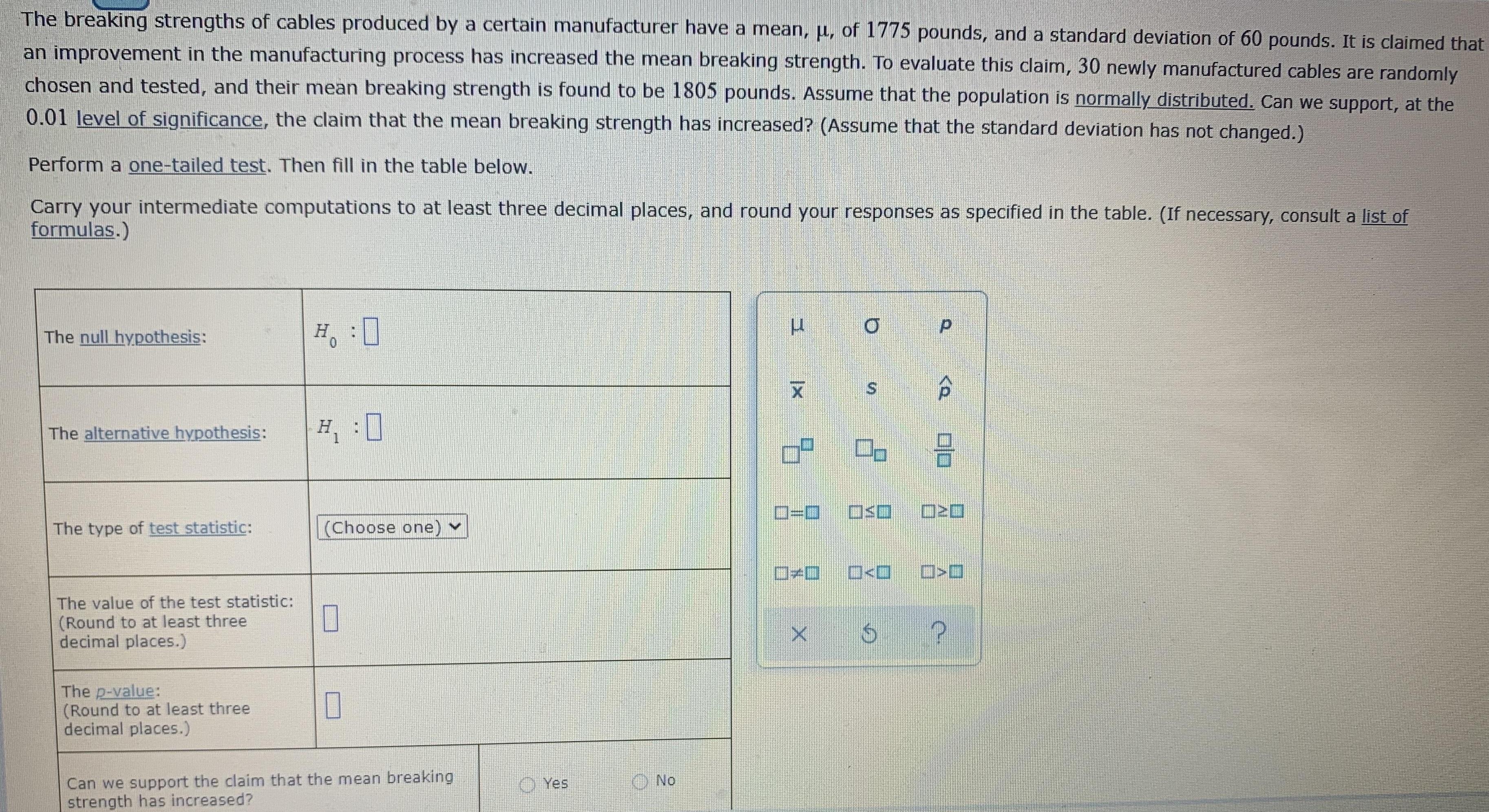
The breaking strengths of cables produced by a certain manufacturer have a mean, u, of 1775 pounds, and a standard deviation of 60 pounds. It is claimed that an improvement in the manufacturing process has increased the mean breaking strength. To evaluate this claim, 30 newly manufactured cables are randomly chosen and tested, and their mean breaking strength is found to be 1805 pounds. Assume that the population is normally distributed. Can we support, at the 0.01 level of significance, the claim that the mean breaking strength has increased? (Assume that the standard deviation has not changed.) Perform a one-tailed test. Then fill in the table below. Carry your intermediate computations to at least three decimal places, and round your responses as specified in the table. (If necessary, consult a list of formulas.) The null hypothesis: #, :0 The alternative hypothesis: H, : O=D The type of test statistic: (Choose one) v