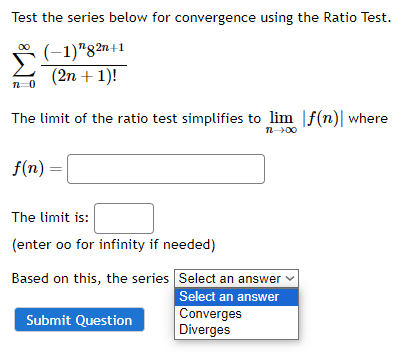
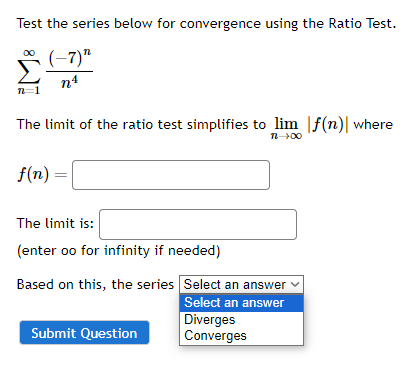
Test the series below for convergence using the Ratio Test. (-1)"82n+1 n-0 (2n + 1)! The limit of the ratio test simplifies to lim f(n) | where f(n) = The limit is: (enter oo for infinity if needed) Based on this, the series |Select an answer v Select an answer Submit Question Converges DivergesTest the series below for convergence using the Ratio Test. (-7) n n4 n=1 The limit of the ratio test simplifies to lim |f(n) | where f(n) = The limit is: (enter oo for infinity if needed) Based on this, the series Select an answer v Select an answer Diverges Submit Question Converges(In n) 3n (In n) Given the series, where an = . Use Root Test to test for convergence. nn a. The limit of the root test simplifies to lim |f(n) | where f(n) = Van 71 +00 f(n) = b. lim f(n)| = (enter oo for infinity if needed) c. Based on the above, the series O converges O diverges