TEXT VERSION:

Net Present ValueUnequal Lives

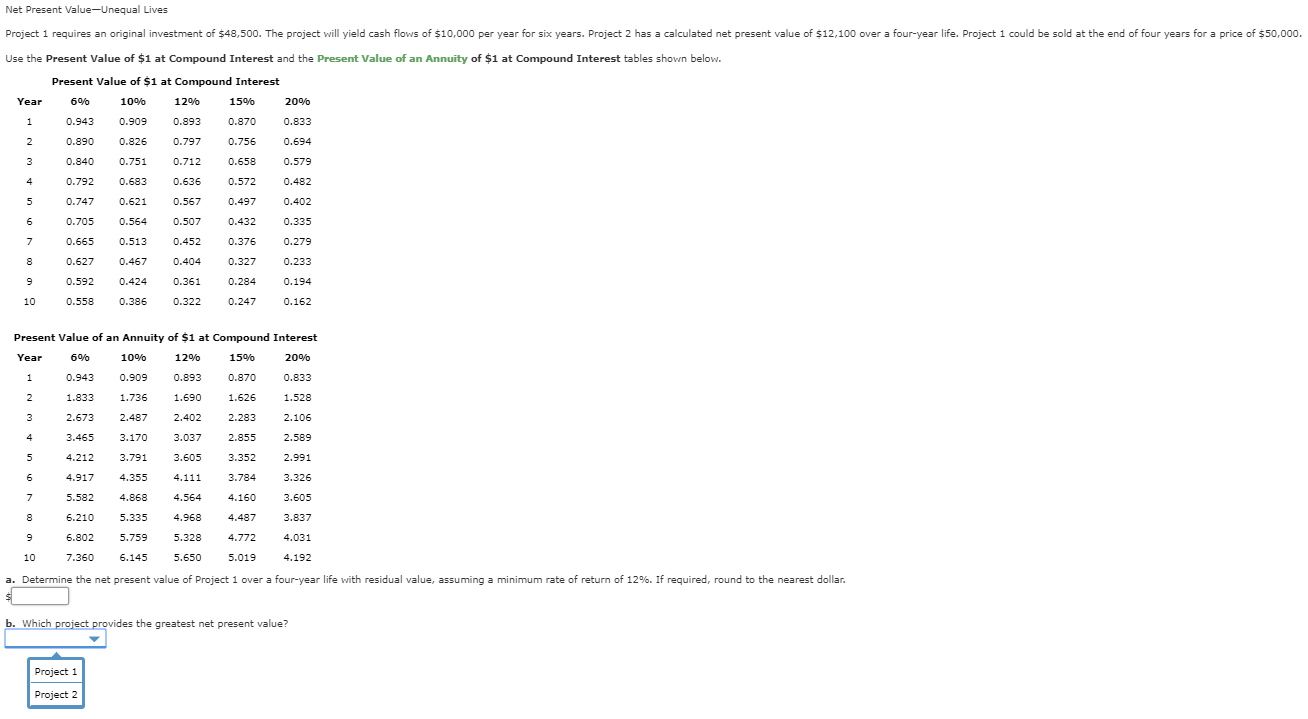
Project 1 requires an original investment of $48,500. The project will yield cash flows of $10,000 per year for six years. Project 2 has a calculated net present value of $12,100 over a four-year life. Project 1 could be sold at the end of four years for a price of $50,000.

Use the Present Value of $1 at Compound Interest and the Present Value of an Annuity of $1 at Compound Interest tables shown below.

Present Value of $1 at Compound Interest
Year	6%	10%	12%	15%	20%
1	0.943	0.909	0.893	0.870	0.833
2	0.890	0.826	0.797	0.756	0.694
3	0.840	0.751	0.712	0.658	0.579
4	0.792	0.683	0.636	0.572	0.482
5	0.747	0.621	0.567	0.497	0.402
6	0.705	0.564	0.507	0.432	0.335
7	0.665	0.513	0.452	0.376	0.279
8	0.627	0.467	0.404	0.327	0.233
9	0.592	0.424	0.361	0.284	0.194
10	0.558	0.386	0.322	0.247	0.162

Present Value of an Annuity of $1 at Compound Interest
Year	6%	10%	12%	15%	20%
1	0.943	0.909	0.893	0.870	0.833
2	1.833	1.736	1.690	1.626	1.528
3	2.673	2.487	2.402	2.283	2.106
4	3.465	3.170	3.037	2.855	2.589
5	4.212	3.791	3.605	3.352	2.991
6	4.917	4.355	4.111	3.784	3.326
7	5.582	4.868	4.564	4.160	3.605
8	6.210	5.335	4.968	4.487	3.837
9	6.802	5.759	5.328	4.772	4.031
10	7.360	6.145	5.650	5.019	4.192

a. Determine the net present value of Project 1 over a four-year life with residual value, assuming a minimum rate of return of 12%. If required, round to the nearest dollar. $

b. Which project provides the greatest net present value?

Net Present Value-Unequal Lives Project 1 requires an original investment of $48,500. The project will yield cash flows of $10,000 per year for six years. Project 2 has a calculated net present value of $12,100 over a four-year life. Project 1 could be sold at the end of four years for a price of $50,000. Use the Present Value of $1 at Compound Interest and the Present Value of an Annuity of $1 at Compound Interest tables shown below. Year M in Present Value of $1 at Compound Interest 6% 10% 12% 15% 20% 0.943 0.909 0.893 0.870 0.833 0.890 0.825 0.797 0.756 0.694 0.840 0.751 0.712 0.658 0.579 0.792 0.683 0.636 0.572 0.482 0.747 0.621 0.567 0.497 0.402 0.705 0.564 0.507 0.432 0.335 0.665 0.513 0.452 0.376 0.279 0.627 0.467 0.404 0.327 0.233 0.592 0.424 0.361 0.284 0.194 0.558 0.386 0.322 0.247 0.162 00 10 M Present Value of an Annuity of $1 at Compound Interest Year 6% 10% 12% 15% 20% 0.943 0.909 0.893 0.870 0.833 1.833 1.736 1.690 1.626 1.528 2.673 2.487 2.402 2.283 2.106 3.465 3.170 3.037 2.855 2.589 4.212 3.791 3.605 3.352 2.991 4.917 4.355 4.111 3.784 3.326 5.582 4.868 4.564 4.160 3.605 6.210 5.335 4.968 4.487 3.837 6.802 5.759 5.328 4.772 4.031 7.360 6.145 5.6505.0194.192 a. Determine the net present value of Project 1 over a four-year life with residual value, assuming a minimum rate of return of 12%. If required, round to the nearest dollar. in 00 b. Which project provides the greatest net present value? Project 1 Project 2