Thanks :) will upvote for the help

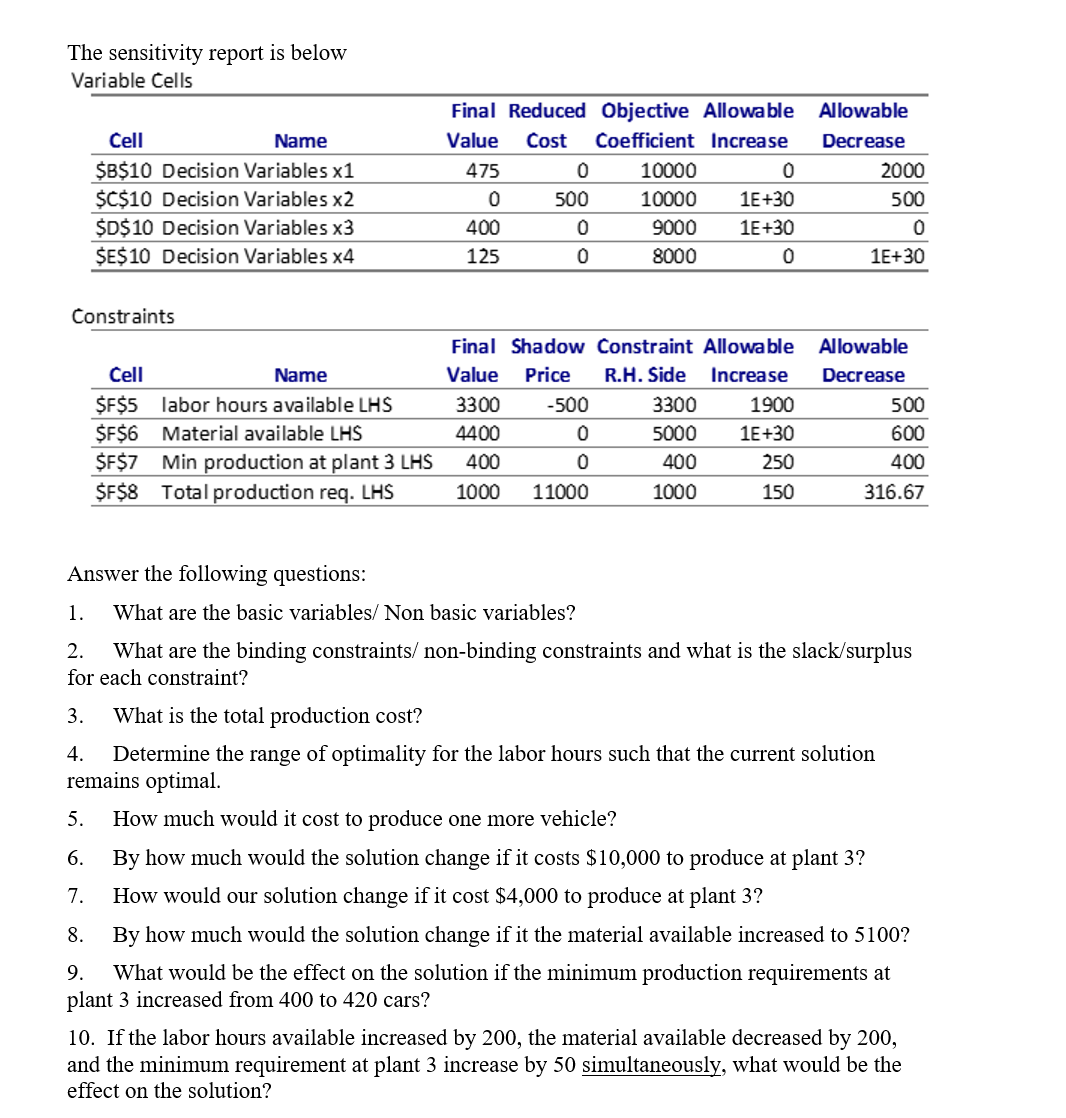
Tucker Inc. needs to produce 900 Tucker automobiles. The company has four production plants. Due to differing workforces, technological advances, and so on, the plants differ in the cost of production of each car. They also use different requirements from labor and raw material at each. The requirements are summarized in the following table: Plant Cost ($) Labor Material 1 10,000 2 4 2 10,000 3 4 3 9,000 4 5 4 8,000 6 4 The labor contract signed requires at least 400 cars to be produced at plant 3. There are 3300 hours of labor and 5000 units of material that can be allocated to the four plants. The objective is to minimize the total production cost. The LP model for this problem is below: Kg number of cars produced at plant 1 X2 : number of cars produced at plant 2 x3=: number of cars produced at plant 3 X4 : number of cars produced at plant 4 Objective: Min Cost Cost = 10,000 X1 + 10,000 x2 + 9,000 x3 + 8,000 x4 Subject to 2x1 + 3x2 4x3 6x4 = 400 Min production at plant 3 x1 + x2 + x3 + x4 >= 1000 Total production requirements x1, x2, x4 >= 0 Non negativity The sensitivity report is below Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $B$10 Decision Variables x1 475 0 10000 0 2000 $C$10 Decision Variables x2 0 500 10000 1E+30 500 $D$10 Decision Variables x3 400 0 9000 1E+30 0 $E$10 Decision Variables x4 125 0 8000 0 LE+30 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $F$5 labor hours available LHS 3300 -500 3300 1900 500 $F$6 Material available LHS 4400 0 5000 1E+30 600 $F$7 Min production at plant 3 LHS 400 0 400 250 400 $F$8 Total production req. LHS 1000 11000 1000 150 316.67 Answer the following questions: 1. What are the basic variables/ Non basic variables? 2. What are the binding constraints/ non-binding constraints and what is the slack/surplus for each constraint? 3. What is the total production cost? 4. Determine the range of optimality for the labor hours such that the current solution remains optimal. 5. How much would it cost to produce one more vehicle? 6. By how much would the solution change if it costs $10,000 to produce at plant 3? 7. How would our solution change if it cost $4,000 to produce at plant 3? 8. By how much would the solution change if it the material available increased to 5100? 9. What would be the effect on the solution if the minimum production requirements at plant 3 increased from 400 to 420 cars? 10. If the labor hours available increased by 200, the material available decreased by 200, and the minimum requirement at plant 3 increase by 50 simultaneously, what would be the effect on the solution