The 0-1 knapsack problem is the following problem:

Input: A knapsack of capacity of L weight units and a list of n items a₁, ..., a_n, where a_i has a value of v_i dollars and weighs w_i units with i = 1, ..., n.

Ouput: A subset of the n items that can be placed in the knapsack to provide the maximum total value.

Which of the following statements are true?

1. Computing V(L) incurs polynomial time.

2. Suppose that the knapsack can hold L weight units of items, where L is a positive integer, and the i-th item has a value v_i and an integer weight W_i with i = 1,2,...n. Let V (k) denote the maximum values of items with total weight

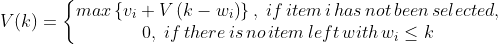Then computing V (L) solves the 0-1 knapsack problem.

3. V (L) can be computed in O(nL) time, which is not a polynomial of the size of the given instance.

4. Sort the items in descending order according to unit values. Select as many top items as possible in the sorted list that can be placed in the knapsack, that is, the total weight of the selected items does not exceed the hold capacity of the knapsack, and there is no more room to hold any more item. This provides a maximum solution to the 0-1 knapsack problem.