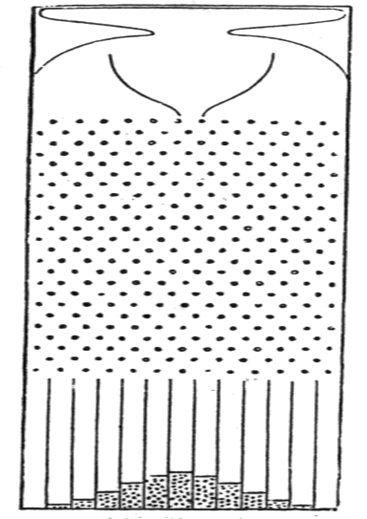
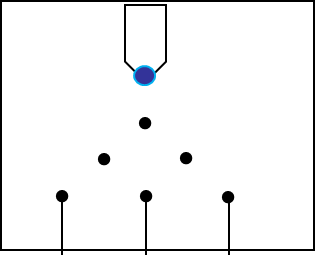
The activity is based on an old experiment coming from the days when probability was first studied with the use of coins, marbles, pegs, cards, or whatever could be found. We will analyze the paths taken by marbles as they fall through a verticaly positioned board containing rows of pegs. Similar probability experiments are frequently simulated in various museums around the world and in games of chance like "Plinko" on The Price is Right game show. In the 1870s, Sir Francis Galton created a device he called a quincunx for studying probability. The device was made up of a vertical board with a chute at the top. The chute was filled with marbles which were dispensed into an array of pegs. The pegs acted as obstructions, forcing the marbles to change direction, the choice of direction being (theoretically) random. At the bottom of the quincunx was a set of bins for catching the marbles. Galton's original sketch of the quincunx, shown at the right, illustrates his setup and shows a possible arrangement of marbles in their bins after completing their journey. Notice how the pegs are arranged as alternating rows so that between two pegs in one row there is a peg in the next row. This falling marble will strike a peg in each row as it progresses. In fact, the word quincunx refers to any arrangement of five objects in a rectangle, one object at each corner and one in the middle. Galton's idea was to use the quincunx to study and explain the final distribution of marbles among the bins. This activity's goal is to have you describe, mathematically and probabilistically, the possible resting places for a marble passing through a quincunx that has one more bin than number of rows of pegs. This activity combines a number of aspects of statistics. First you will use a specific probability distribution to model the possible outcomes of a particular experiment, one with its roots in randomness. Second, you will use your model to predict the outcome of the experiment. Lastly, this project will employ simulation to replicate the experiment allowing you to compare your theortical results with an actual experimental outcome.

\f\f