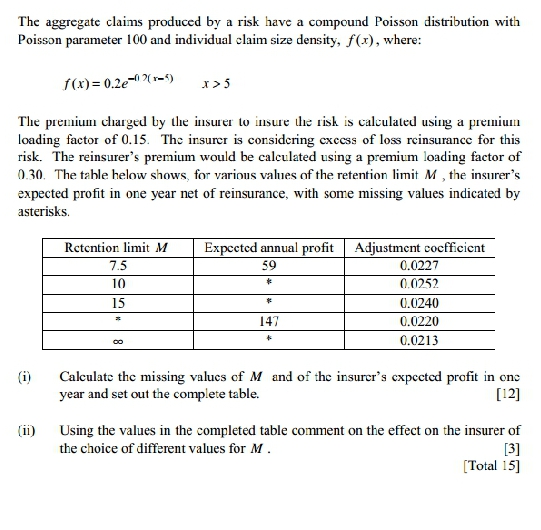
The aggregate claims produced by a risk have a compound Poisson distribution with Poisson parameter 100 and individual claim size density, f(x), where: f(x)=0.2e-02(x-5) x>5 The premium charged by the insurer to insure the risk is calculated using a premium loading factor of 0.15. The insurer is considering excess of loss reinsurance for this risk. The reinsurer's premium would be calculated using a premium loading factor of 0.30. The table below shows, for various values of the retention limit M, the insurer's expected profit in one year net of reinsurance, with some missing values indicated by asterisks. (i) (ii) Retention limit M 7.5 10 15 = 00 Expected annual profit Adjustment coefficient 59 * * 147 * 0.0227 0.0252 0.0240 0.0220 0.0213 Calculate the missing values of M and of the insurer's expected profit in one year and set out the complete table. [12] Using the values in the completed table comment on the effect on the insurer of the choice of different values for M. [3] [Total 15]