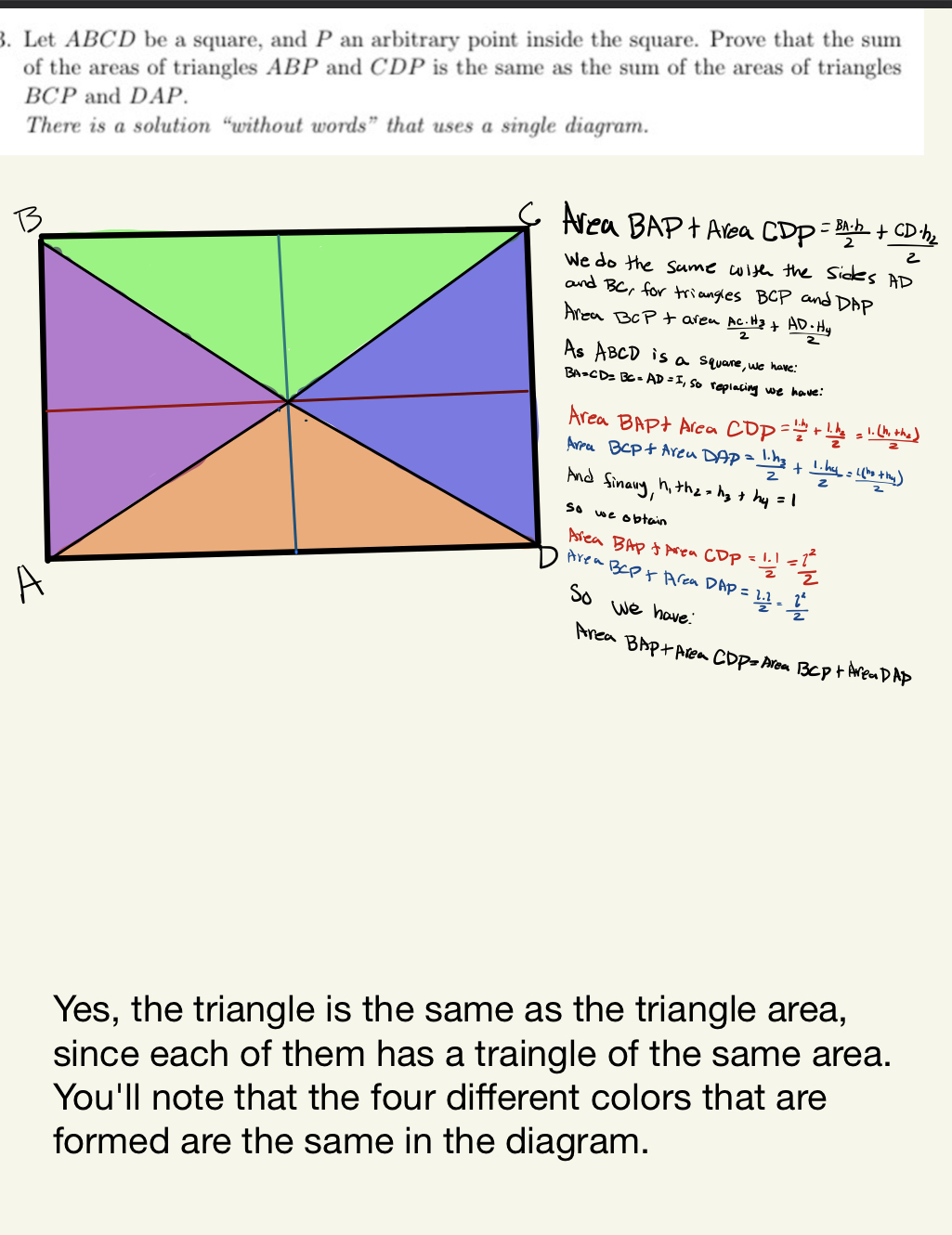
Question: the algebra solution is correct. the diagram solution is not correct, because the triangles with the same color are not congruent, only if point p
the algebra solution is correct. the diagram solution is not
correct, because the triangles with the same color are not congruent, only if point p is the center of the square.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


