The algorithm below takes two positive integers input, a and b, and returns product (ab). Use loop invariant to prove the algorithms correctness. You can use the notations: prod[i], x[i], and y[i] to represent the values of prod, x, and y after while loop executed i times. Consider the quantity prod[i] + x[i]y[i].

Sort the functions listed below from asymptotically smallest to largest. Do not turn in proofs just smallest to largest.

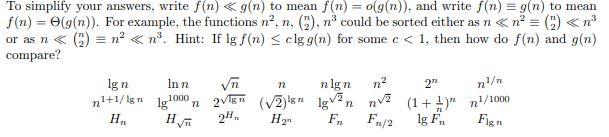
prod0,xMuLTIPLY(a,b):a,yb while x>0 if x is odd prodprod+y xx/2 yy+y return prod To simplify your answers, write f(n)g(n) to mean f(n)=o(g(n)), and write f(n)g(n) to mean f(n)=(g(n)). For example, the functions n2,n,(n2),n3 could be sorted either as nn2(n2)n3 or as n(n2)n2n3. Hint: If lgf(n)clgg(n) for some c