The almost universally used algorithm to compute a, where a > 0, is the recursion

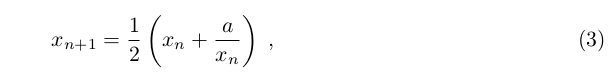easily obtained by means of Newtons method for the function f (x) = x 2 a.

The trick for doing this is to use Newtons method to compute 1 a , and then obtain a by multipling by a. Write down your recur- sion formula for computing 1 a in a manner similar to (3). This formula should only involve addition/subtraction, multiplication and division by 2.

Try you algorithm on the problem of computing 5. As an initial guess use x 0 = 0.5. Report the values of x 0 , x 1 ,. . . , x 5 in a nice table and verify that your algorithm is working by comparing these numbers to the true value of 5

I've tried:

clc clear all iteration = 100; A = 5; a=1/A; x=a/2; xn=1; tolerance = 10e-16; f =@x .5*(xn+a/xn) while f ~= sqrt(A)* tolerance x(n+1) = f(x(n)); end

x(n+1)

but I've been banging my head and am now probably so confused that I'm missing the obvious.

2 3 rt rt