Question: The answer is not those two!!!!!!!!! The answer is not those two!!!!!!!!! The answer is not those two!!!!!!!!! The answer is not those two!!!!!!!!! The

The answer is not those two!!!!!!!!! The answer is not those

The answer is not those two!!!!!!!!!

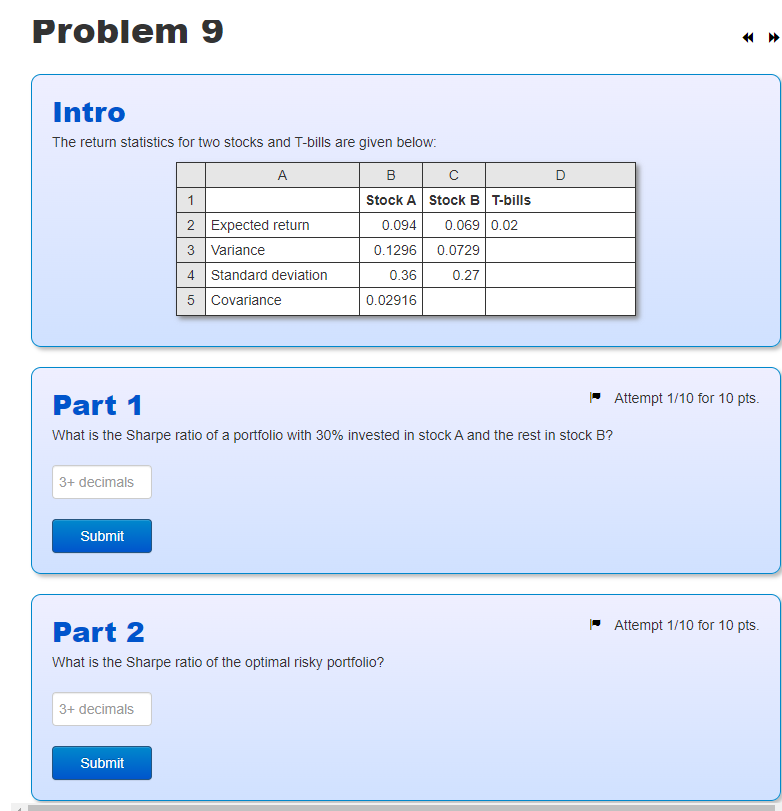
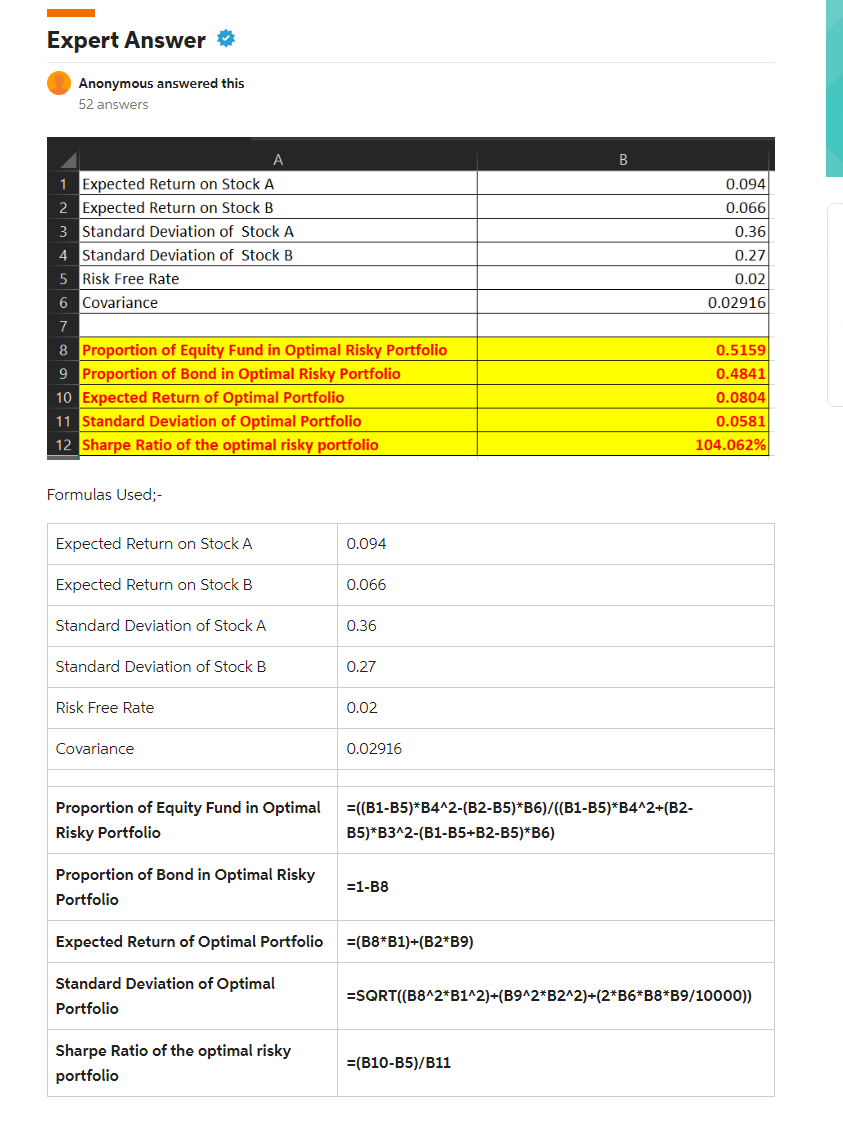
Problem 9 D Intro The return statistics for two stocks and T-bills are given below: A B 1 Stock A Stock B T-bills 2 Expected return 0.094 0.069 0.02 3 Variance 0.1296 0.0729 4 Standard deviation 0.36 0.27 5 Covariance 0.02916 Part 1 Attempt 1/10 for 10 pts. What is the Sharpe ratio of a portfolio with 30% invested in stock A and the rest in stock B? 3+ decimals Submit Attempt 1/10 for 10 pts. Part 2 What is the Sharpe ratio of the optimal risky portfolio? 3+ decimals Submit Expert Answer Anonymous answered this 52 answers B 0.094 0.066 0.36 0.27 0.02 0.02916 1 Expected Return on Stock A 2 Expected Return on Stock B 3 Standard Deviation of Stock A 4 Standard Deviation of Stock B 5 Risk Free Rate 6 Covariance 7 8 Proportion of Equity Fund in Optimal Risky Portfolio 9 Proportion of Bond in Optimal Risky Portfolio 10 Expected Return of Optimal Portfolio 11 Standard Deviation of Optimal Portfolio 12 Sharpe Ratio of the optimal risky portfolio 0.5159 0.4841 0.0804 0.0581 104.062% Formulas Used: - Expected Return on Stock A 0.094 Expected Return on Stock B 0.066 Standard Deviation of Stock A 0.36 Standard Deviation of Stock B 0.27 Risk Free Rate 0.02 Covariance 0.02916 Proportion of Equity Fund in Optimal Risky Portfolio =((B1-B5)*B4^2-(B2-B5)*B6)/((B1-B5)*B4^2+(B2- B5)*B3^2-(B1-B5-B2-B5)*86) Bond in Optimal Risky Proportion Portfolio =1-B8 Expected Return of Optimal Portfolio =(B8*B1)+(B2*B9) Standard Deviation of Optimal Portfolio =SQRT((B8^2*B1^2)+(B9^2*B2^2)+(2*B6*B8*B9/10000)) Sharpe Ratio of the optimal risky portfolio =(B10-B5)/B11 Vic Bepected return - 0.3x0.094 +0.7% 0.069. = 0.0282 +0.0483 Rp = 0.0765 Standard deviation of portfolio - WA=0.3, W8 -0.7, =0-1996, B =0:0729 'A=0.36, B=0-37, PAB=0.02916 - SCWA) + (p) & (88) + 2X WAX LWB X A X BX UAB + (0-3)* X0.1296+ (0.7 x 0729 + 2x0.3X0 1780.36X0.87 + 8 2 xo-02916 >10.01166 +0.03572 +0.00119 0.04857 - 92.04 7. or 0-2204 => RE = 0.02 Rp=0.0765 0 o=0-2204 Sharpe ratio= Rp. Rp 0.0765-0.02 0.0565 0.2204 0.2204 = 0.256 Problem 9 D Intro The return statistics for two stocks and T-bills are given below: A B 1 Stock A Stock B T-bills 2 Expected return 0.094 0.069 0.02 3 Variance 0.1296 0.0729 4 Standard deviation 0.36 0.27 5 Covariance 0.02916 Part 1 Attempt 1/10 for 10 pts. What is the Sharpe ratio of a portfolio with 30% invested in stock A and the rest in stock B? 3+ decimals Submit Attempt 1/10 for 10 pts. Part 2 What is the Sharpe ratio of the optimal risky portfolio? 3+ decimals Submit Expert Answer Anonymous answered this 52 answers B 0.094 0.066 0.36 0.27 0.02 0.02916 1 Expected Return on Stock A 2 Expected Return on Stock B 3 Standard Deviation of Stock A 4 Standard Deviation of Stock B 5 Risk Free Rate 6 Covariance 7 8 Proportion of Equity Fund in Optimal Risky Portfolio 9 Proportion of Bond in Optimal Risky Portfolio 10 Expected Return of Optimal Portfolio 11 Standard Deviation of Optimal Portfolio 12 Sharpe Ratio of the optimal risky portfolio 0.5159 0.4841 0.0804 0.0581 104.062% Formulas Used: - Expected Return on Stock A 0.094 Expected Return on Stock B 0.066 Standard Deviation of Stock A 0.36 Standard Deviation of Stock B 0.27 Risk Free Rate 0.02 Covariance 0.02916 Proportion of Equity Fund in Optimal Risky Portfolio =((B1-B5)*B4^2-(B2-B5)*B6)/((B1-B5)*B4^2+(B2- B5)*B3^2-(B1-B5-B2-B5)*86) Bond in Optimal Risky Proportion Portfolio =1-B8 Expected Return of Optimal Portfolio =(B8*B1)+(B2*B9) Standard Deviation of Optimal Portfolio =SQRT((B8^2*B1^2)+(B9^2*B2^2)+(2*B6*B8*B9/10000)) Sharpe Ratio of the optimal risky portfolio =(B10-B5)/B11 Vic Bepected return - 0.3x0.094 +0.7% 0.069. = 0.0282 +0.0483 Rp = 0.0765 Standard deviation of portfolio - WA=0.3, W8 -0.7, =0-1996, B =0:0729 'A=0.36, B=0-37, PAB=0.02916 - SCWA) + (p) & (88) + 2X WAX LWB X A X BX UAB + (0-3)* X0.1296+ (0.7 x 0729 + 2x0.3X0 1780.36X0.87 + 8 2 xo-02916 >10.01166 +0.03572 +0.00119 0.04857 - 92.04 7. or 0-2204 => RE = 0.02 Rp=0.0765 0 o=0-2204 Sharpe ratio= Rp. Rp 0.0765-0.02 0.0565 0.2204 0.2204 = 0.256

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

All questions must be done utilizing microsoft excel and the attachment template with answers must be sent back to me. 1. QUESTION 1 Identify a use of cash from below. Choose only one. decrease in...

please I need help ASAP on these? can anyone assist Not allowed. This test can only be taken once. Force Completion This test can be saved and resumed at any point until time has expired. The timer...

I am in need of assistance in answering these questions. I only have 2 hrs and 30 minutes. Thank you so much for your help! QUESTION 1 ABC Company sells 2,014 chairs a year at an average price per...

Question 1 Which of the following cash flows are NOT considered in the calculation of the initial outlay for a capital investment proposal? Interest expense related to financing a project Cost of...

I need help with the attached homework.. I am really lost... 1. What is the Modified Internal Rate of Return (MIRR) for the following cash flows? Assume that the required rate of return is 4% Year...

Attached please find a word document to be solved. Q U EST I O N 1 In New York, you can exchange $1 for 0.8984 or 0.7589. Suppose that, in Berlin, 1 costs 1.1618. How much profit can you earn on...

HI! Can I please get your help on the attached? Please do not share this information anywhere. Thank you! Nicole Question 1 1. Compute the cash cycle based on the following information: Average...

1 ABC Corp. issued 15-year bonds 2 years ago at a coupon rate of 10.6%. The bonds make semi-annual payments. If these bonds currently sell for 97% of par value, what is the YTM? Note: Enter your...

Question 1 Security A has expected return of 17.6% and beta of 1.4. If the risk-free rate is 6%, what is the reward-to-risk rate for Security A? Enter your answer as a percentage rounded off to two...

Answer Question: Part A. Question 1 Security A has expected return of 17.6% and beta of 1.4. If the risk-free rate is 6%, what is the reward-to-risk rate for Security A? Enter your answer as a...

I have some bad news. Goose is separating from his wife Carole. This is going to be so hard on Rooster, their 10 year old son. They have agreed for Carole to stay in the house with Rooster. Goose has...

let z denote the probability that a randomly selected respondent supports current laws legalizing abortion, predicted using gender of the respondent (G = 0, male; G = 1, female), religious...

On September 1 of Year 1, a company paid $1,800 cash to rent office space for one year beginning immediately. Assuming the company's accounting year ends on December 31, the amount of rent expense...

ONE (15 MARKS) Kate and Robert are in partnership as manufacturers of plastic bottles. Kate is responsible for the factory operations and Robert is responsible for sales. The following trial balance...