the answer of ( iii ) the objective function value = 2x30+5x75= 435... why ?

why 2x30+$ 4 x 75 is wrong ?

I have the answer of abcdefg, but I don't know where the formula come from...

I know noting about "Sensitivity Analysis", please explain to me easily( my english is bad ).

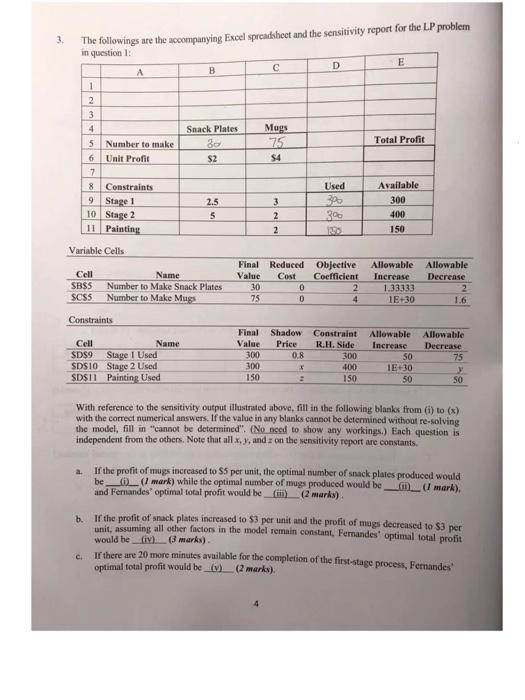
3 The followings are the accompanying Excel spreadsheet and the sensitivity report for the LP problem in question 1: E D B 1 2 3 4 Snack Plates Mugs 5 Number to make 30 75 Total Profit 6 Unit Profit S2 $4 7 8 Constraints Used Available 9 Stage 1 2.5 3 300 10 Stage 2 5 2 30- 400 11 Painting 2 150 Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease SBSS Number to Make Snack Plates 30 0 2 1.33333 2 $C$5 Number to Make Mugs 75 0 4 1E+30 1.6 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $D$9 Stage 1 Used 300 0.8 300 SO 75 SDS10 Stage 2 Used 300 400 IE+30 $D$11 Painting Used 150 150 50 SO With reference to the sensitivity output illustrated above, fill in the following blanks from (i) to (x) with the correct numerical answers. If the value in any blanks cannot be determined without re-solving the model, fill in cannot be determined". (No need to show any workings. Each question is independent from the others. Note that all x, y, and on the sensitivity report are constants. If the profit of mugs increased to $5 per unit, the optimal number of snack plates produced would be_10_(1 mark) while the optimal number of mugs produced would be G0_1 mark) and Fernandes optimal total profit would be in) (2 marks) b. If the profit of snack plates increased to 53 per unit and the profit of mugs decreased to $3 per unit, assuming all other factors in the model remain constant, Fernandes optimal total profit would be in marks) If there are 26 more minutes available for the completion of the first stage process, Fernandes optimal total profit would be (v)__(2 marks). c. a 0 30 (ii) 75 (iii) S435 The increase of the coefficient of X, in the objective function is within the allowable increase The optimal solution would not change: X, - 30 (1) and X, - 25.000). The objective function value - 2 x 30+ 5 x 75 S435 (ii) b. Using the 100% rule: 1/1.333 + 1/1.6 - 137.5% > 100%. The optimal solution may have changed. Therefore, the objective function value cannot be determined (iv). c. Since the increase of 20 minutes is within the allowable increase of 50 minutes, the shadow price (S0.8) remains unchanged in the first constraint. Fernandes' optimal profit = $360 + (0.8 x 20) - $376 (v) (iv) Cannot be determined (v) 376 (vi) o (vii) 100 (viii) 0.8 (ix) 75 (x) Jo d. Since the second constraint is non-binding, the shadow price (x) equals to Q (vi) The allowable decrease of the right-hand side of the constraint. y - 400 - 300 - 100 (vii) e. The reduced cost of X - 4 - (30.8+2**+2 *2)=0 Since .x=04-2.4 -0-2:02:=1.6: -0.8 (viii) C. The new reduced cost of X = 4 - 3 * 0.8 +30+2 *0.8) = 0. There is no change in the reduced cost of X, and therefore the optimal value of X, remains at 25 (ix) 2. The new reduced cost of X, -4 -14%0.8+2x0+ 2* 0.8) = -0.8. The reduced cost of X, changes from 0 to a negative value, the optimal value of X, therefore will be set at the lower bound 0 (x) need to nse excel