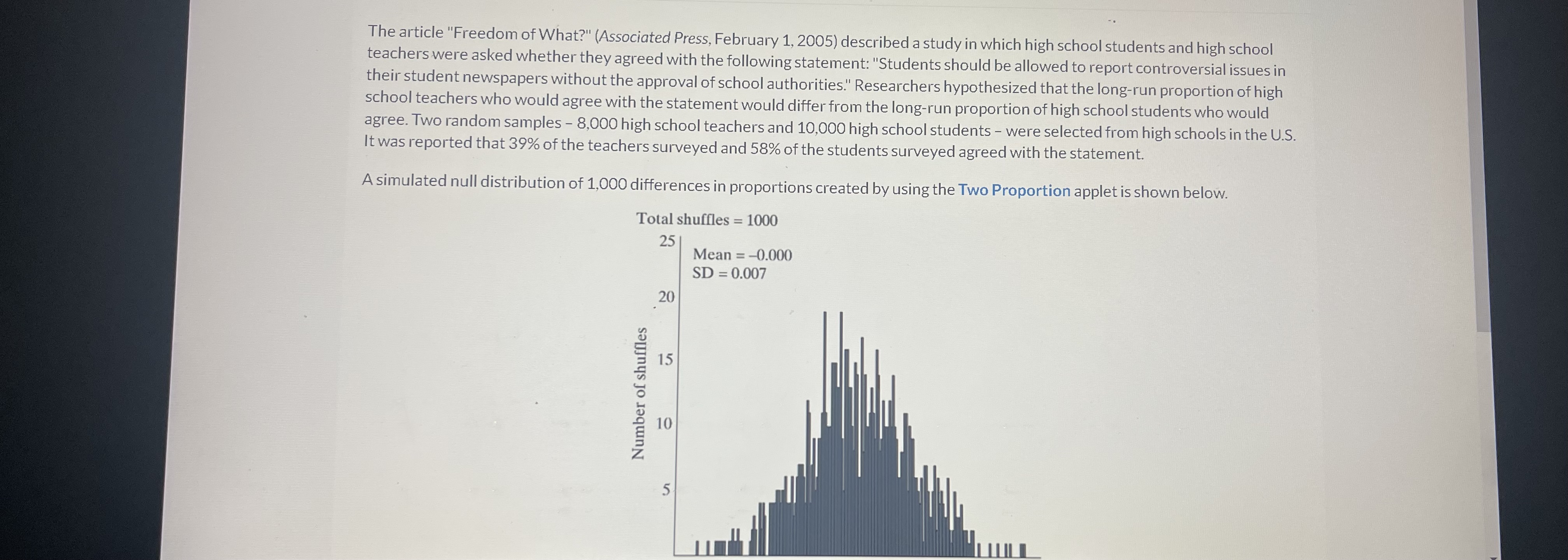
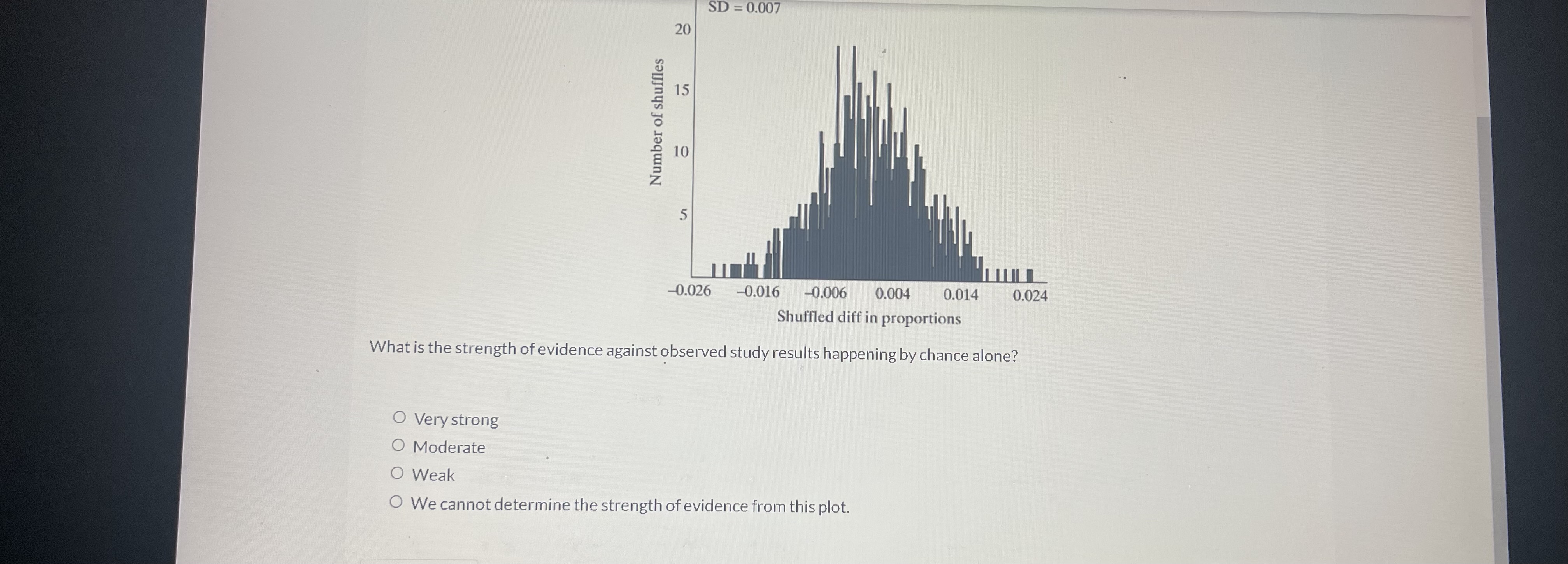
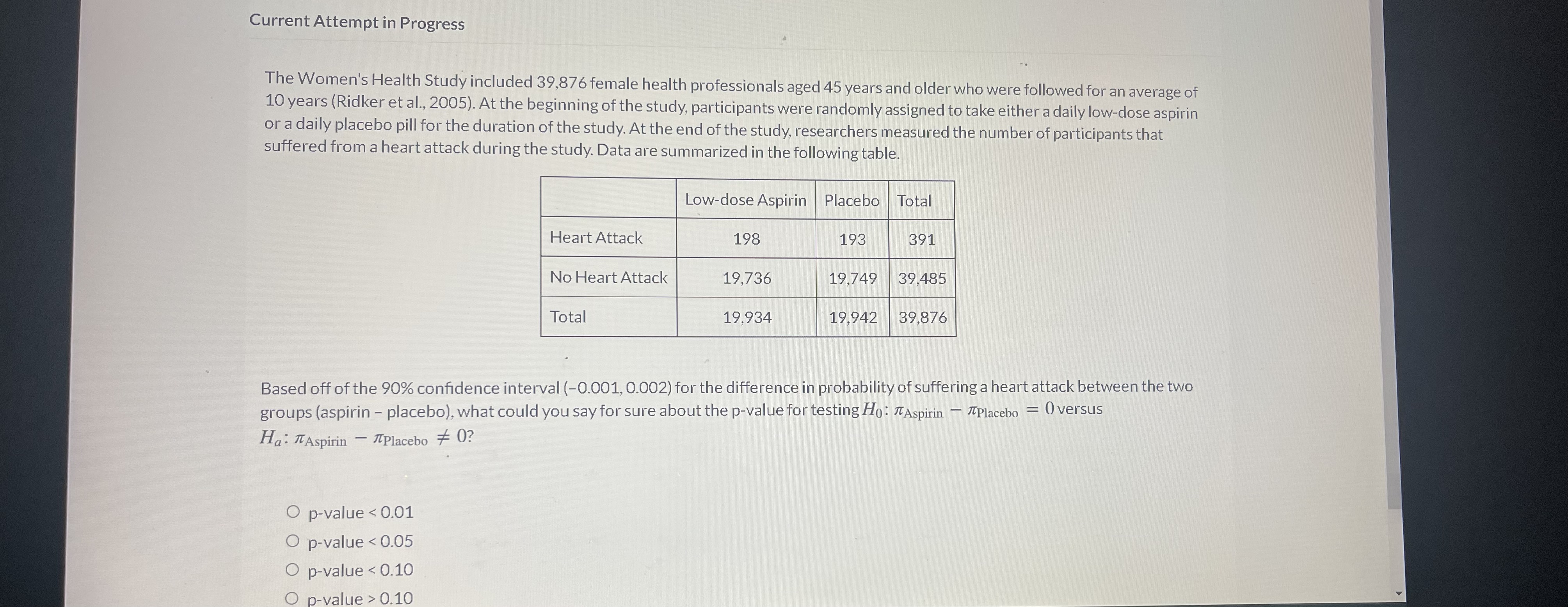
The article "Freedom of What?" (Associated Press, February 1, 2005) described a study in which high school students and high school teachers were asked whether they agreed with the following statement: "Students should be allowed to report controversial issues in their student newspapers without the approval of school authorities." Researchers hypothesized that the long-run proportion of high school teachers who would agree with the statement would differ from the long-run proportion of high school students who would agree. Two random samples - 8,000 high school teachers and 10,000 high school students - were selected from high schools in the U.S. It was reported that 39% of the teachers surveyed and 58% of the students surveyed agreed with the statement. A simulated null distribution of 1,000 differences in proportions created by using the Two Proportion applet is shown below. Total shuffles = 1000 25 Mean = -0.000 SD = 0.007 20 15 Number of shuffles 10 USD = 0.007 20 15 Number of shuffles 10 UI m LULL 0.026 -0.016 -0.006 0.004 0.014 0.024 Shuffled diff in proportions What is the strength of evidence against observed study results happening by chance alone? O Very strong O Moderate O Weak O We cannot determine the strength of evidence from this plot.The article "Freedom of What?" (Associated Press, February 1, 2005) described a study in which high school students and high school teachers were asked whether they agreed with the following statement: "Students should be allowed to report controversial issues in their student newspapers without the approval of school authorities." Researchers hypothesized that the long-run proportion of high school teachers who would agree with the statement would differ from the long-run proportion of high school students who would agree. Two random samples - 8,000 high school teachers and 10,000 high school students - were selected from high schools in the U.S It was reported that 39% of the teachers surveyed and 58% of the students surveyed agreed with the statement. The study concluded that "in the U.S., a higher percentage of high school students believe controversial issues should be reported without approval of school authorities than high school teachers." Is this conclusion justified? Yes, because the sample sizes were large. O No, since we did not survey all high school students and high school teachers in the U.S. Yes, because the 2SD 95% confidence interval for the difference in long-run proportion who would agree with the statement between Students and Teachers (Students - Teachers) is entirely greater than zero. O No, because the 2SD 95% confidence interval for the difference in long-run proportion who would agree with the statement between Students and Teachers (Students - Teachers) is entirely greater than zero.The Women's Health Study included 39,876 female health professionals aged 45 years and older who were followed for an average of 10 years (Ridker et al., 2005). At the beginning of the study, participants were randomly assigned to take either a daily low-dose aspirin or a daily placebo pill for the duration of the study. At the end of the study, researchers measured the number of participants that suffered from a heart attack during the study. Data are summarized in the following table. Low-dose Aspirin Placebo Total Heart Attack 198 193 391 No Heart Attack 19,736 19,749 39,485 Total 19,934 19,942 39,876 Is a theory-based approach appropriate to evaluate the relationship between whether an individual took aspirin or a placebo and whether an individual suffers a heart attack? Yes, since 39,876 is larger than 20. Yes, since 391 and 39,485 are both greater than 10. O Yes, since 198, 193, 19,736, 19,749 are all greater than 10. O No, since a simulation-based approach is always appropriate.Current Attempt in Progress The Women's Health Study included 39,876 female health professionals aged 45 years and older who were followed for an average of 10 years (Ridker et al., 2005). At the beginning of the study, participants were randomly assigned to take either a daily low-dose aspirin or a daily placebo pill for the duration of the study. At the end of the study, researchers measured the number of participants that suffered from a heart attack during the study. Data are summarized in the following table. Low-dose Aspirin Placebo Total Heart Attack 198 193 391 No Heart Attack 19,736 19,749 39,485 Total 19,934 19,942 39,876 Based off of the 90% confidence interval (-0.001, 0.002) for the difference in probability of suffering a heart attack between the two groups (aspirin - placebo), what could you say for sure about the p-value for testing Ho: It Aspirin - Placebo = 0 versus Ha: T Aspirin - Placebo # 0? O p-value 0.10A 2003 study reported in the Journal of Consumer Affairs examined how well consumers protect themselves from identity theft. The study surveyed a random sample of 61 college students and 59 non-students, and asked each participant, "Have you used personal information (such as birth date, pet name, etc.) when creating a password?" For the students, 22 agreed with this statement, while 30 of the non-students agreed. If we increased the confidence level from 95% to 99%, all else remaining the same, the center of the confidence interval would O increase. O decrease. O remain the same