Question: The average revenue is defined as the function R(x) (x) (x > 0) Prove that if a revenue function R(x) is concave downward (R(x)

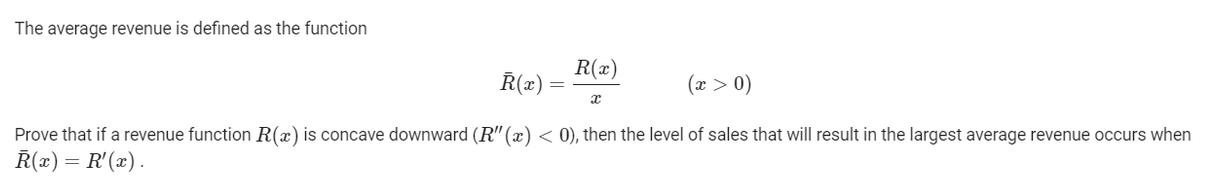
The average revenue is defined as the function R(x) (x) (x >

The average revenue is defined as the function R(x) (x) (x > 0) Prove that if a revenue function R(x) is concave downward (R"(x) < 0), then the level of sales that will result in the largest average revenue occurs when R(x) = R'(x).

Step by Step Solution

★★★★★

3.40 Rating (144 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Elizabeth Burke wants to develop a model to more effectively plan production for the next year. Currently, PLE has a planned capacity of producing 9,100 mowers each month, which is approximately the...

Prove that if a > 1/2, then is differentiable at (0, 0). ylog(2 y x y) (x, y) (0, 0) (0.0) f(a. y)

Prove that if A is singular, then adj A is singular. First show that if A is singular, then A(adj A) = O.

Prove that if A attracts B, then A repels B .

I need help on C programming please: bold texts are my assignment below that i wrote some codes on main.c, sporkpr0file.c and sporkprofile.h but in some lines, i am cinfused. thank for your help....

Teuro5 For the year ending December 31, 2021, the Company's income statement is as follows: Revenues $1,093,000 Expenses: Cost Of Goods Sold ($206,000) Administrative Costs ( 152,000) Amortization...

In a certain town 60% of the households own mutual funds, 40% own individual stocks, and 20% own both mutual funds and individual stocks. 1. The proportion of households that own mutual funds but not...

Please carry out calculations to two decimals before rounding off, as a general rule. Also, please show your work where possible. 1.Here is a linear demand function:Q = 12 - .5PFind its price...

Here is a linear demand function:Q = 12 - .5PFind its price function by inverting the demand function.Then find its total revenue function by multiplying through by Q.EXAMPLE:The linear demand...

he following data represent the total revenue R (in dollars) received from selling x bicycles at Tunneys Bicycle Shop (a) Find the average rate of change in revenue from x = 25 to x = 150 bicycles....

When a mutual fund company charges a fee of 0.47% on its index funds, its assets in the fund are $45 billion. When it charges a fee of 0.17%, its assets in the fund are $296 billion. (a) Let x denote...

A star has an average density of p = 1050.0 kg/m^3 and a radius of R = 24500.0 km. What is the maximum gravitational acceleration this star can create?

Lydia is starting a new business. She expects to earn a before-tax rate of return equal to 8% and she plans to operate the business for a minimum of 3 years. Lydia's business operates in an industry...

dar = ( x - 1 ) ( x - 4 ) 2 ( + - 7 ) 2 ( + - 8 ) . d t Compute the following l i m i t s ( s h o w your computations ) . I f the l i m i t does not exist write DNE. ( a ) I f ( 0 ) = 2 . 5 , then l...

One of the important factors in determining population growth rates is the birthrate per 1000 individuals in a population. The dotplot shows the birthrates per 1000 individuals (rounded to the...

An experimenter wishes to compare eight treatments in blocks of four runs. Find a BIRD with 14 blocks and = 3.

What externalities exist when there is a casino, and how might those externalities be dealt with in a way that would allow a casino while also mitigating the externalities?

An open tank has a constant inflow of 20 ft 3 /s. A 1.0-ft-diameter drain provides a variable outflow velocity V out equal to (2gh) ft/s. What is the equilibrium height heq of the liquid in the tank?

Research has shown that approximately 1 woman in 600 carries a mutation of the BRCA1 gene. About 60% of women with this mutation develop breast cancer. Find the probability that a randomly selected...

Find the population mean or sample mean as indicated. Sample: 18, 11, 7, 9, 20. The arithmetic mean of a variable is computed by determining the sum of all the values of the variable in the data set,...

Efficiency Wages and the Threat of Firing Workers: In our treatment of labor demand earlier in the text, we assumed that firms could observe the marginal revenue product of workersand thus would hire...

maxis company in 2019, 2020,2021 (need to find based on following 1. Current Ratio 2. Quick Ratio 3. Average Collection Period (ACP) 4. Total Asset Turnover 5. Debt Ratio 6. Debt Equity Ratio 7. Net...

Year Quarter Location CarClass Revenue NumCars 2018 Q1 Airport Economy 1011191 5650 2018 Q1 Downtown Economy 943509 5965 2017 Q4 Airport Economy 926382 5122 2016 Q3 Downtown Economy 777155 5280 2017...

It is Snapchat A which is found in your course pack. You are to turn in an excel a) excel spreadsheet with formulas for calculations. The spreadsheet should show cash flow, WACC calculation, firm...

List three specific parts of the Case Guide, Objectives and Strategy Section (See below) that you had the most difficulty understanding. Describe your current understanding of these parts. Provide...

Please help with this problem! 1. Consider a car wash that can serve up to two cars. Customers arrive according to a Poisson process of rate per hour. The service time for one car is exponentially...