the beam's section modulus. This is a property based solely on the geometry of the beam, specifically the moment of inertia and the centroid:

$S=\frac{\text{I}}{c}$

Once a loading is specified, we can use the flexure formula with the maximum bending moment, $M_{\text{m}\text{a}\text{x}},$ to specify a lower bound on the section modulus:

$S_{\text{r}\text{e}\text{q}\text{u}\text{i}\text{r}\text{e}\text{d}}=\frac{M_{\text{m}\text{a}\text{x}}}{{}_{\text{a}\text{l}\text{l}\text{o}\text{w}}}$

Where the maximum bending stress, ${}_{\text{a}\text{l}\text{l}\text{o}\text{w}\text{,}},$ is a parameter generally given in the design specifications.

The shear specification,

${}_{\text{a}\text{l}\text{l}\text{o}\text{w}}\frac{V_{\text{m}\text{a}\text{x}}Q}{It}$

is generally less specific than the bending$-$moment specification, so it is used as the secondary design consideration.

Figure

$3$ of $3$

Correct

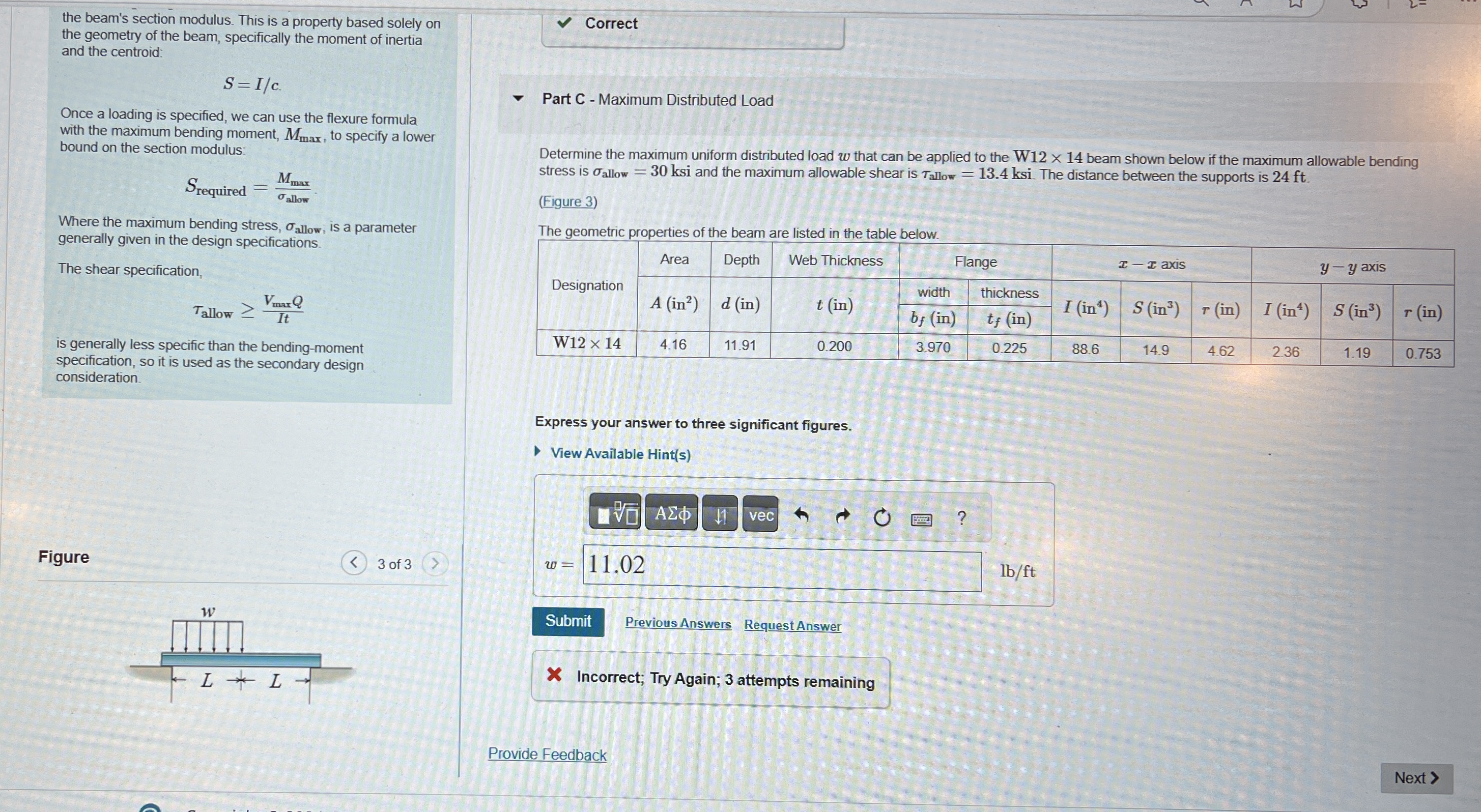
Part C $-$ Maximum Distributed Load

Determine the maximum uniform distributed load $w$ that can be applied to the $W1214$ beam shown below if the maximum allowable bending stress is ${}_{\text{a}\text{l}\text{l}\text{o}\text{w}}=30$ksi and the maximum allowable shear is ${}_{\text{a}\text{l}\text{l}\text{o}\text{w}}=13\mathrm{.}4$ksi. The distance between the supports is $24$ ft $.$

$($Figure $3)$

The geometric properties of the beam are listed in the table below.

$\backslash$table$[[$Designation$,$Area,Depth,Web Thickness,Flange,$x-x$ axis,$y-y$ axis$],[$ in ${?}^2),d($in$),t($in$),$width,thickness,$I(i{n}^4),S(i{n}^3),r($in$),I(i{n}^4),$ in ${?}^3),r($in$)],[b_f($in$),t_f($in$)],[$W$1214,4\mathrm{.}16,11\mathrm{.}91,0\mathrm{.}200,3\mathrm{.}970,0\mathrm{.}225,88\mathrm{.}6,14\mathrm{.}9,4\mathrm{.}62,2\mathrm{.}36,1\mathrm{.}19,0\mathrm{.}753]]$

Express your answer to three significant figures.

View Available Hint$($s$)$

Previous Answers

Request Answer

Provide Feedback