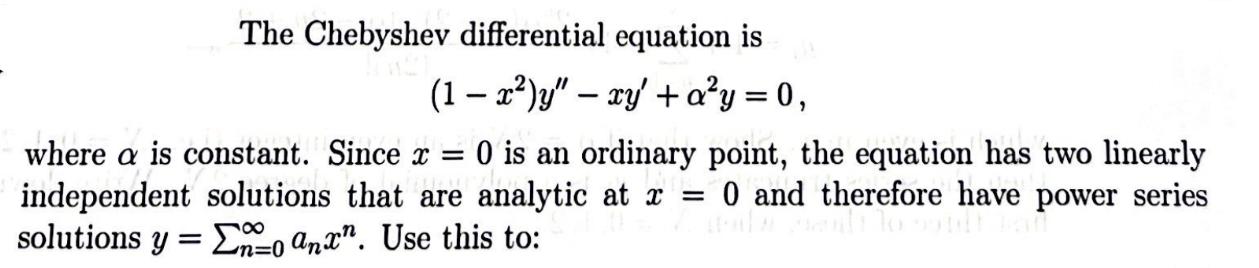
The Chebyshev differential equation is - (1 x)y" xy' + ay = 0, where a is constant. Since x = 0 is an ordinary point, the equation has two linearly independent solutions that are analytic at x = 0 and therefore have power series 8 solutions y = 0 anx". Use this to: (a) Find the recurrence relation an+2 = (n-a)OH ESOS HATED BM 1, ., an for n=0,1 (8) alls buil (1) aotsapano (n+2) (n + 1) lot and lo 1) 200 and use this to construct the two solutions y and y2. One solution y has ao 0, a =0, and only even powers of x. Show that its coefficients satisfy of 2. Show that its com moisillows strupo has 300 m ((2m-2) - a) a2m-2 for m = 1, 2,.... offeme 2m (2m-1) a2m = The second solution y2 has ao = 0, a 0, and only odd powers of x. Show that its coefficients satisfy to nonpo situs of (x-x1)" ((2m - 1) - a) 09 0198-110102m+1 = a2m-1 for m = 1, 2,....(b) (2m+1)2m Hope 19 Write down the first few terms of each solution. oqzd un-2(x-5)+"UT (9) = ... N+1 (b) Show that if a is an even integer, so that a = 2N for N 1,2, when m = all terms in the series for y are zero after the term in xN. This gives solutions that are even polynomials in x. Find the first three even polynomials (N = 0, 1, 2). (c) Show that if a is an odd integer, so that a = 2N+1 for N = 0, 1, 2,..., when m = N + 1 all terms in the series for y are zero after the term in x2N+1. This gives solutions that are odd polynomials in x. Find the first three odd polynomials (N = 0,1,2).