The code given is below

code in text format

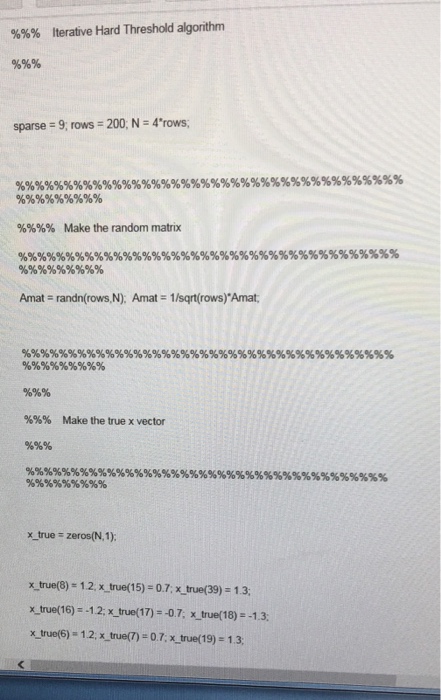
%%% Iterative Hard Threshold algorithm

%%%

sparse = 9; rows = 200; N = 4*rows;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%% Make the random matrix

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Amat = randn(rows,N); Amat = 1/sqrt(rows)*Amat;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%

%%% Make the true x vector

%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

x_true = zeros(N,1);

x_true(8) = 1.2; x_true(15) = 0.7; x_true(39) = 1.3;

x_true(16) = -1.2; x_true(17) = -0.7; x_true(18) = -1.3;

x_true(6) = 1.2; x_true(7) = 0.7; x_true(19) = 1.3;

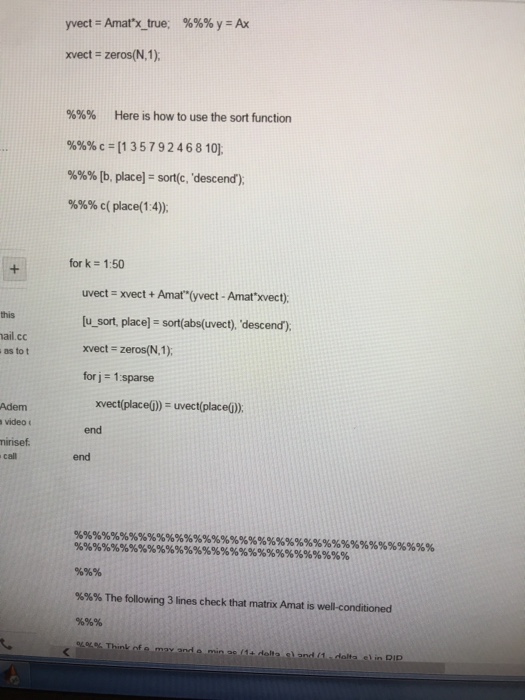
yvect = Amat*x_true; %%% y = Ax

xvect = zeros(N,1);

%%% Here is how to use the sort function

%%% c = [1 3 5 7 9 2 4 6 8 10];

%%% [b, place] = sort(c, 'descend');

%%% c( place(1:4));

for k = 1:50

uvect = xvect + Amat'*(yvect - Amat*xvect);

[u_sort, place] = sort(abs(uvect), 'descend');

xvect = zeros(N,1);

for j = 1:sparse

xvect(place(j)) = uvect(place(j));

end

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%

%%% The following 3 lines check that matrix Amat is well-conditioned

%%%

%%% Think of e_max and e_min as (1+ delta_s) and (1 - delta_s) in RIP

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

A_submat = Amat(:,[39,15,16,17,18,19,6,7,8]);

eigenvalues = eig(A_submat'*A_submat);

e_max = max(eigenvalues); e_min = min(eigenvalues); [e_max, e_min]

%%% Compare the true values with the predicted values.

%%% The predicted values are in the vector xvect.

%%% Show the first 50 values of the true values and predicted values.

[x_true([1:50],1) xvect([1:50],1)]

MAT 388/488 Assignment 3 Due Wednesday, April 26th at the beginning of class in the last lecture, we learned the lterative Hard Thresholding (IHT) algorithm. In this exercise, you will use Matlab to explore lHT. Using the Matlab code that was sent to you in an email, copy and paste the code exactly as given into your Matlab, then run the program. This program creates a 9-sparse vector z E RNO and a random matrix A with m a 200 rows and N 4m columns. It also makes the vector y E Rao, where y Az. Using the vector y E Rao and the matrix A, the algorithm reconstructs the 9-sparse vector r, after 50 iterations of lHT. The output of the program are: (1) the first 50 entries of the true vector z and the first 50 entries of the reconstructed vector, (2) the error. The reconstructed vector is xvect. Following the first 50 entries of these two vectors (the true one versus the recon- structed), is the error e, where ll true reconstructed Iltruella Run the Matlab program a few times and you will see that IHT can reconstruct the 9-sparse vector when the matrix A has 200 rows and 800 columns. Part 1. Now change the number of rows of the matrix to 100, while keeping N Ann. Throughout this part of the exercise, continue to keep the number of columns to be exactly 4 times the number of rows. Run the program a few times and you will notice IHT fails to reconstruct the 9-sparse vectors. That means, as you decrease the number of rows from 200 to 100, while keeping the number of columns to be 4 times the number of rows, the performance of IHT gets worse and worse, until IHT fails to reconstruct the true vector