The code is not working. Thank you!

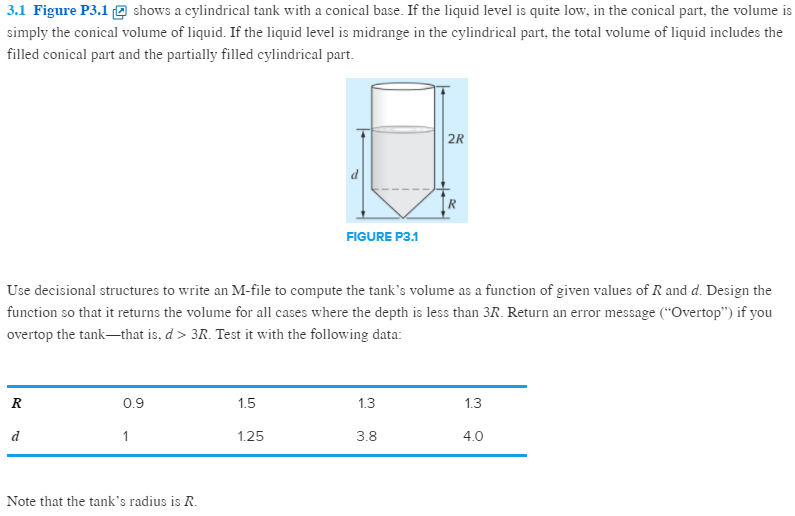
Fill out the order of the flow chart.

CODE:

function Vol = Chapra_Problem_3p1( d, R )

%% Input

% d: depths of liquid filling tanks, independent variable (1 x N)

% R: Radii of cylindrical tanks, parameter (1 x N)

%

%% Output

% Vol: Volumes computed for liquid filling tanks (1 x N)

% Set Vol(-) to -1 for 'Overtop'.

% Write your function here.

if d

Vol = (pi*d^3)/3;

else if d

V1 = (pi * R.^3)/3;

V2 = pi * R^2*(d-R);

Vol = V1+V2;

else

Vol = 'overtop';

end

end

end

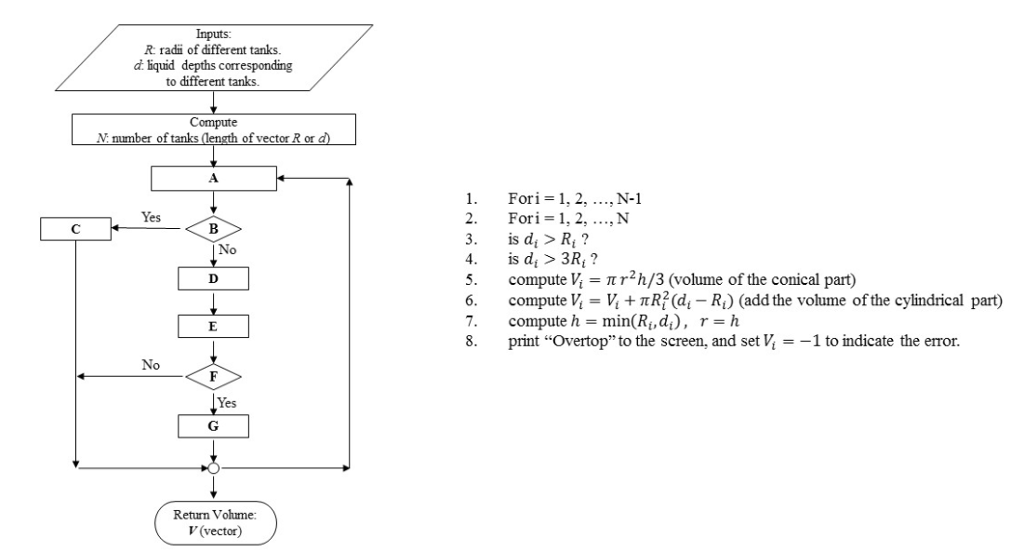
3.1 Figure P3.1 shows a cylindrical tank with a conical base. If the liquid level is quite low, in the conical part, the volume is simply the conical volume of liquid. If the liquid level is midrange in the cylindrical part, the total volume of liquid includes the filled conical part and the partially filled cylindrical part 2R FIGURE P3.1 Use decisional structures to write an M-file to compute the tank's volume as a function of given values of R and d. Design the function so that it returns the volume for all cases where the depth is less than 3R.Return an error message C"Overtop") if you overtop the tank-that is, d> 3R. Test it with the following data: 0.9 1.5 1.3 1.3 1.25 3.8 4.0 Note that the tank's radius is R