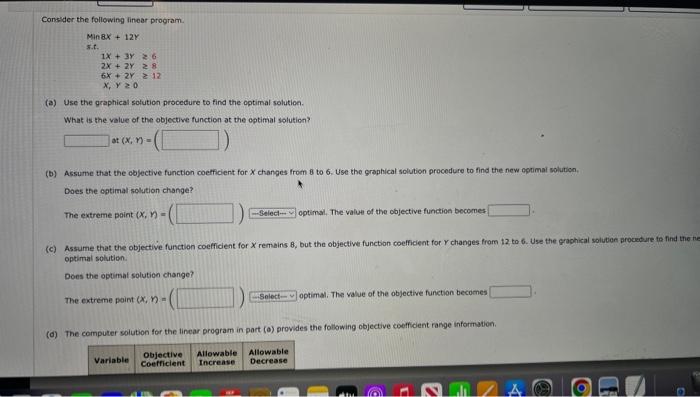
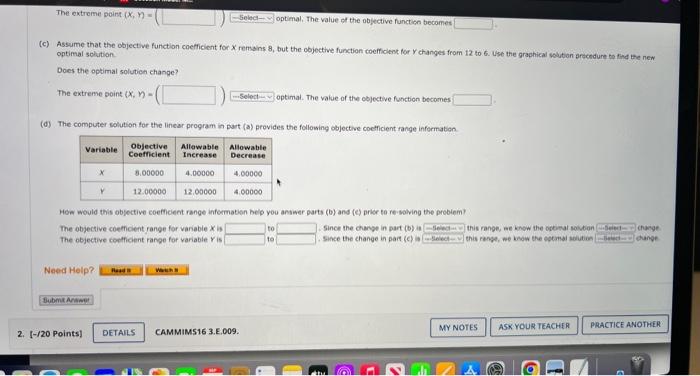
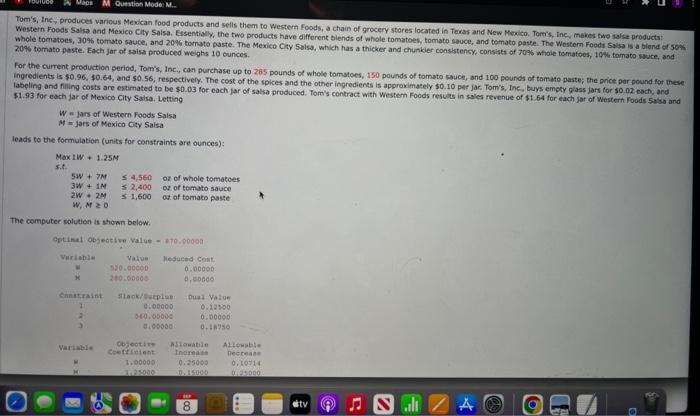
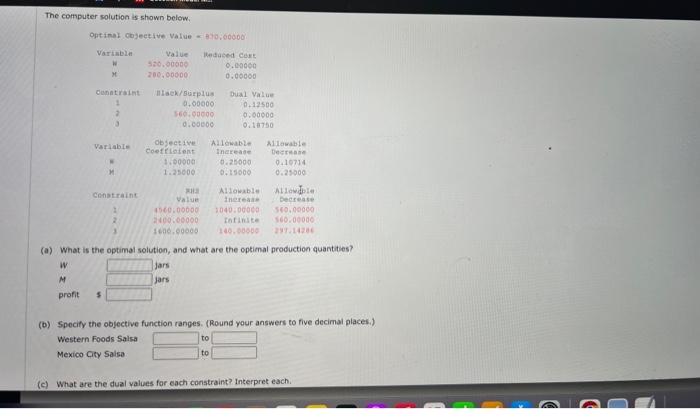
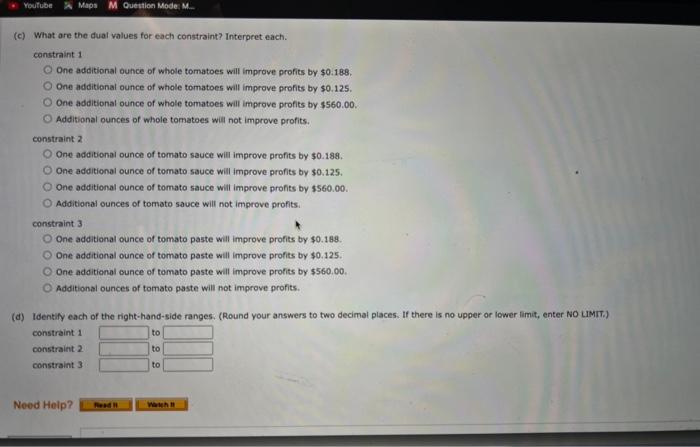
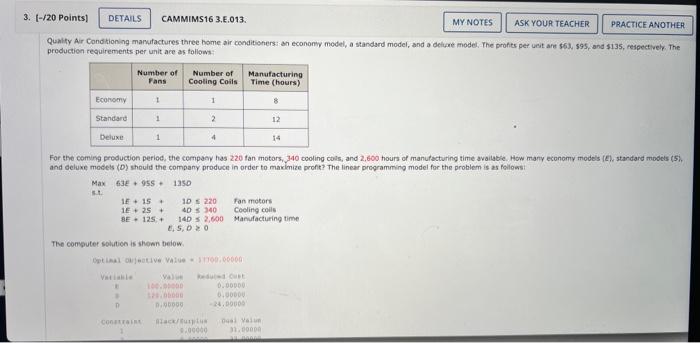
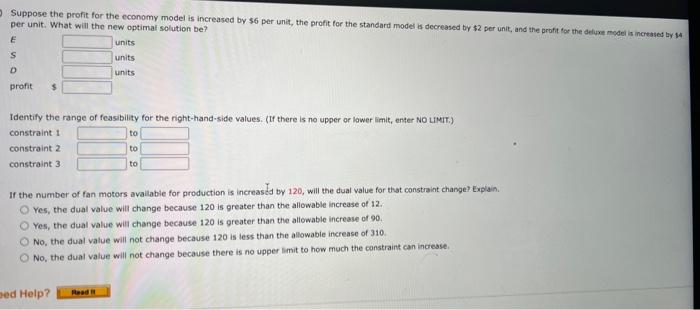
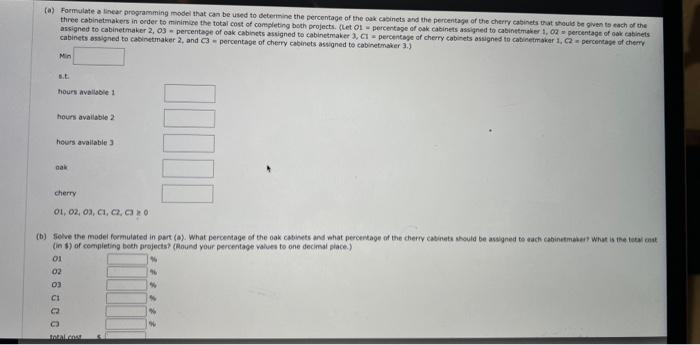
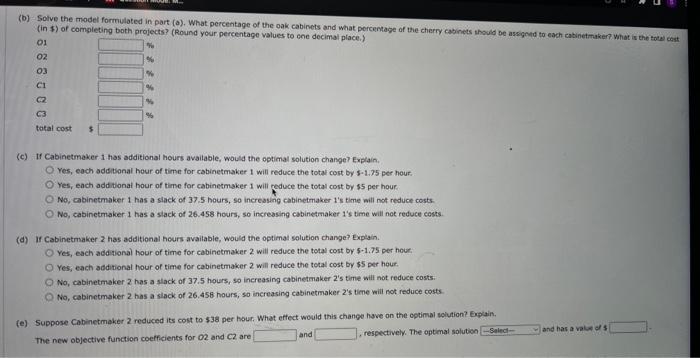
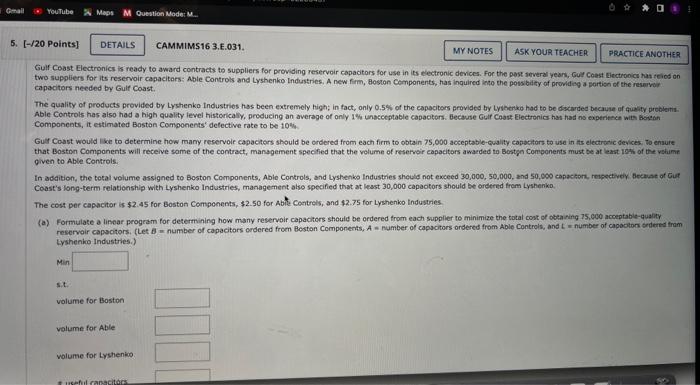
The computer solution is shown below (a) Identify the range of optimality for each objective function coefficient. (If there is no upper or lower ime, enter No LMIt). ESDtototo Suppose the profit for the economy model is increased by $6 per unit, the profit for the standard model is decreased by $2 per unit, and the profit for the delume model is increased by 14 per unit. What will the new optimal solution be? Identify the range of feasibility for the right-hand-side values. (If there is no upper or lower limit, enter No Limit.) constraint 1 to constraint 2 constraint 3 to to If the number of fan motors avaliable for production is increastd by 120 , will the dual value for that constraint change? Explain. Yes, the dual value will change because 120 is greater than the allowable increase of 12. Yes, the dual value will change because 120 is greater than the allowable increase of 90. No, the dual value will not change because 120 is less than the allowabie increase of 310 . No, the dual value will not change because there is no upper limit to how much the constraint can increase. Consider the following linear program. Minex+12ys.t.1X+3y62X+2y86x+2y12xry0 (a) Use the graphical solution procedure to find the optimal solution. What is the value of the objective function at the optimal solution? at (x,n)= (b) Assume that the objective function coefficient for x changes from 8 to 6 , Use the graphical solution procedure to find the new optimal solution. Does the optimal solution change? The extreme paint (x,y)= optimsil, The value of the objective function becomes optimal solution. Does the optimat solution change? The extreme point x,n= optimal. The value of the objective function becomes (d) The computer solution for the linear program in part (o) provides the following objective coefficient range information. The computer solution is shown below. Optinal Cojective Value - Alo, 00000 (a) What is the optimal solution, and what are the optimal production quantities? (b) Specify the objective function ranges. (Round your answers to five decimal places.) Western Foods Salsa to Mexico City Salsa to (c) What are the dual yalues for each constraint? Interpret each. (c) What are the dual values for each constraint? Interpret each. constraint 1 One additional ounce of whole tomatoes will improve profits by $0.188. One additienal ounce of whole tomatoes will improve profits by $0.125. One additional ounce of whole tomatoes will improve profits by $560.00. Additional ounces of whole tomatoes will not improve profits. constraint 2 One additional ounce of tomate sauce will improve profits by 50.188. One additional ounce of tomato sauce will improve profits by $0.125. Additional ounces of tomato sauce will not improve profits: constraint 3 One additional ounce of tomato paste will improve profits by $0.188. One additional ounce of tomato paste will improve profits by $0.125. One additional ounce of tomato paste will improve profits by $560,00. Additional ounces of tomato paste will not improve profits. (d) Identify each of the right-hand-side ranges. (Round your answers to two decimal places. If there is no upper or lower limit, enter No LIMIT.) constraint 1 constraint 2 constraint 3 20% tomato paste. Each Jor of saisa produced weighs 10 cunces. $1.93 for each jar of Menico City Salsa. Letting WnjarsofWesternFoodsSalsaH=jarsofMexicoCtySalsa. leads to the formulation (units for constraints are ounces): Max1W+1.25M5.t.5W+7N4,560ozofwholetomatoes3W+1M2,400ozoftematosauce2W+2M1,600ozoftomatopaste The computer solution is shown below. Optimal objective Value - 170 wo000 cabinets assigned to cabinetmaker 2 , and C3= percentage of cherry cabinets assigned to cabinetmaker 3.3 (in s) of compieting beh projects? (Round your percentage values to one decimal place.) ol 02 o3 C1 c Gulf Coast Electronics is ready to award contracts to suppliers for providing reservoir capactors for use in its electronic devices. For the post several yeans, GuI Coest Electrooicu has reios on capacitors needed by Gulf Coast. The quality of products provided by Lyshenko Industries hes been extremely high; in fact, only 0.5% of the capaciters provided by lyinerixo had to be discarded because of quaity preblenis. Components, it estimated Boston Components' defective rate to be 10%. that Boston Components will receive same of the contract, manygement specified that the volume of reservoir capacitors awarded to Bostgo Conponents must be at least Igh of the vetumn given to Able Controls. In adaition, the total volume assigned to Boston Components, Able Controls, and Lyshenko Industries sheula not exceed 30,000, 50,000, and 50,000 capactorh, renpectivex. fecauat of Gut Coast's long-term relationship with Lyshenico Industries, management also specified that at least 30,000 capaotors should be ordered frem Lyshenka. The cost per capacitor is $2.45 for Boston Componemts, $2.50 for A bit. Contrels, and $2.75 for Lyshenko Industries. (a) Formulate a linear program for determining how many reservoir capactiters should be ordered from each supplier to minimize the total cont of obeaning 75 , coo acceptabie-quahty reservoir capscitors. (Let B= number of capacitors ordered froen Beston Components, A= number of capacitors ordered from Able Controls, and L= number of capocton ordered tram Lyshenko Industries.) s.t. volume for Boston valume for Able volume for Lyshenko: A linear programming computer package is needed. For example, Cabinetmaker. 1 etimates it wa take 50 hours to complete all the cak cabinets and 60 hours to complete all the cherry cabinats, Howeve, Cabinetmouer 1 oniy has 40 houn only complete 40/60=0.67, or 67%, of the cheny cabinets if is worked only on cherry cabinets: (o) Formulate a linear programming model that can be used to determint the percenkage of the oak cabinets and the percentage of the cherry cabioets that thouit be given to eash of the production requirements per unit are as tollows: and deluxe modes (D) should the company produce in order to maximize profi? The linear prepramming model for the problem is as followsi Max63E+955+135015+15+10220fanmotors1E+25+40340Coelingcolls8E+125+1402,600Manufacturingtime The computer solitice is shown beiow Bosten Corsoenents capositar Asie Contrels capacitan twaherkin indswines capsctors level nave? the optimal salutios movid reman the same. Cenvderation fave in the solation in wart (a)? keduong the requiremest will net change the tetat cont of obeaining the reserveir capaction. (b) Solve the model formulated in part (o). What percentage of the oak cabinets and what percentage of the cherry cabinets thovid be assigned to each cabinetimaker? What is the toeve cast (in 5) of completing both projects? (Round your percentage values to ene decimal place.) o1 O2 o3 CI c. C3 (c) If Cabinetmaker 1 has additional hours avaitable, would the optimal solution change? Explain. Yes, each additbonal hour of time for cabinetmaker 1 wili reduce the total cost by 51.75 per hour: Yes, each additional hour of time for cabinetmaker 1 will reduce the total cost by $5 per hour. No, cabinetmaker 1 has a slack of 37,5 hours, so increasing cabinetmaker 1 's time will not reduce costs. No, cabinetmaker 1 has a slack of 26.458 hours, so increasing cabinetmaker 1 's time will not reduce costs. (d) If Cabinetmaker 2 has additional hours available, would the optimal solution change? Explain. Yes, each additional hour of time for cabinetmaker 2 will reduce the total cost by 5-1.75 per hour: Yes, each additional hour of time for cabinetmaker 2 will reduce the total cost by $5 per hour. No, cabinetmaker 2 has a slack of 37.5 hours, so increasing cabinetmaker 2 's time will not reduce costs. No, cabinetmaker 2 has a slack of 26.458 hours, so increasing cabinetmaker 2 's time will not reduce costs. (e) Suppose Cabinetmaker 2 reduced its cost to 538 per hour. What effect would this change have on the optimal selution? Epplain. The new objective function coefficients for O2 and C2 are and , respectively. The optinal solution and has a vale of 5 (c) Assume that the objective function coefficient for X remains 8 , but the objective function coefficient for Y changes from 12 to 6 . Use the graphical solution arscedure to find the new optimal solution. Does the optimal solution change? The extreme point (x,n)=( optimal. The value of the objective function becomes (d) The computer solution for the linear program in part (a) provides the following objective coeticient range information. Hen would this objective coefficent range infermatien belo you answer parts (b) and (e) prise te reisolving the prebiem? The objective coetholent range for variabie x is to Since the charye in part (b) is this range, ne know the osberat novbon charge The objective comticient range for variable Y is to - since the change in part (C) is this range, no know the socmal sobition