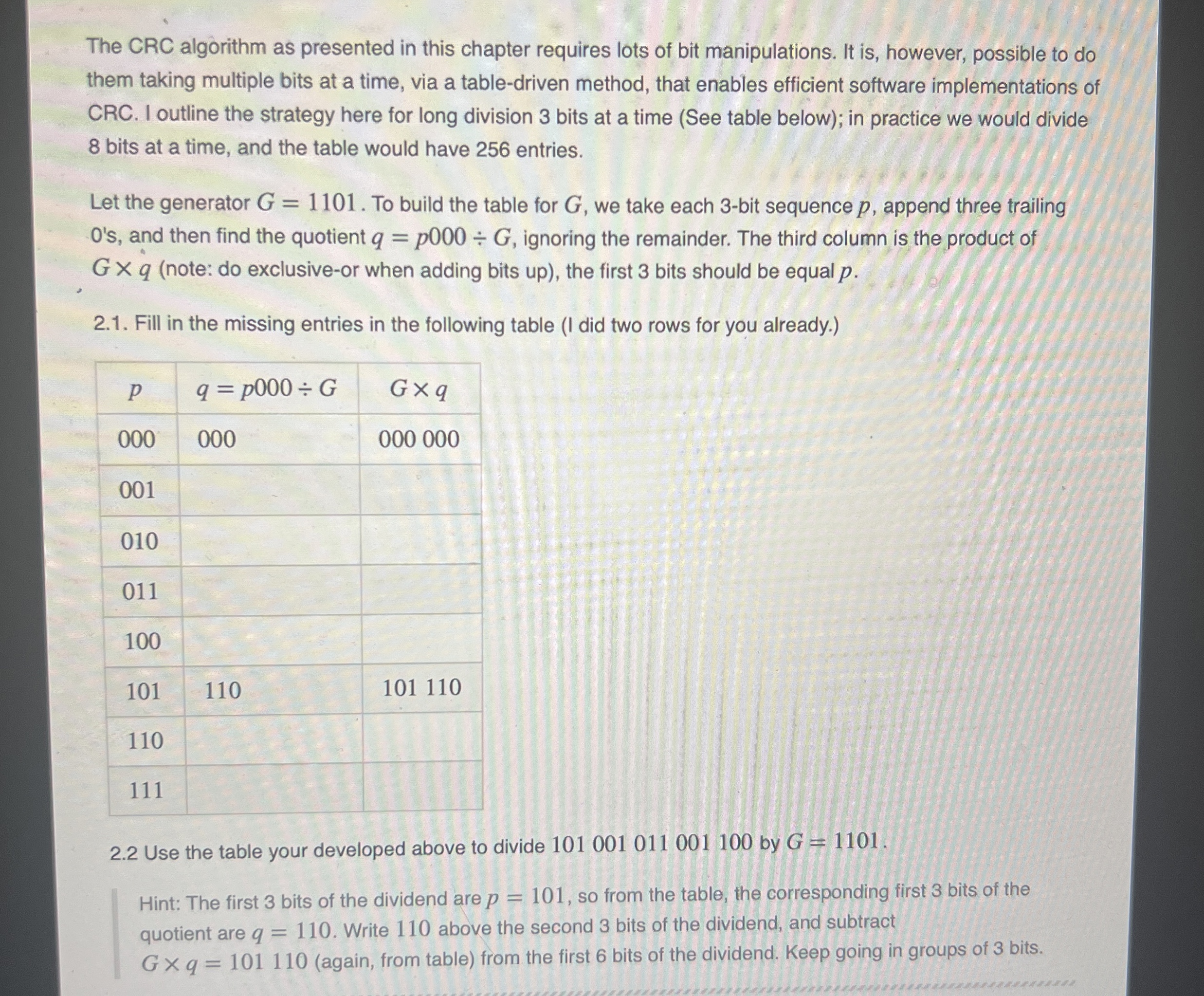
The CRC algorithm as presented in this chapter requires lots of bit manipulations. It is$,$ however, possible to do them taking multiple bits at a time, via a table$-$driven method, that enables efficient software implementations of CRC$.$ I outline the strategy here for long division $3$ bits at a time $($See table below$)$; in practice we would divide $8$ bits at a time, and the table would have $256$ entries.

Let the generator $G=1101.$ To build the table for $G,$ we take each $3-$bit sequence $p,$ append three trailing $0\text{'}$s$,$ and then find the quotient $q=p000G,$ ignoring the remainder. The third column is the product of $Gq($note: do exclusive$-$or when adding bits up$),$ the first $3$ bits should be equal $p.$

$2\mathrm{.}1.$ Fill in the missing entries in the following table $($I did two rows for you already.$)$

$\backslash$table$[[p,q=p000G,Gq$