The demand for widgets is 60 per day. Each worker can product the widgets at the following rates:

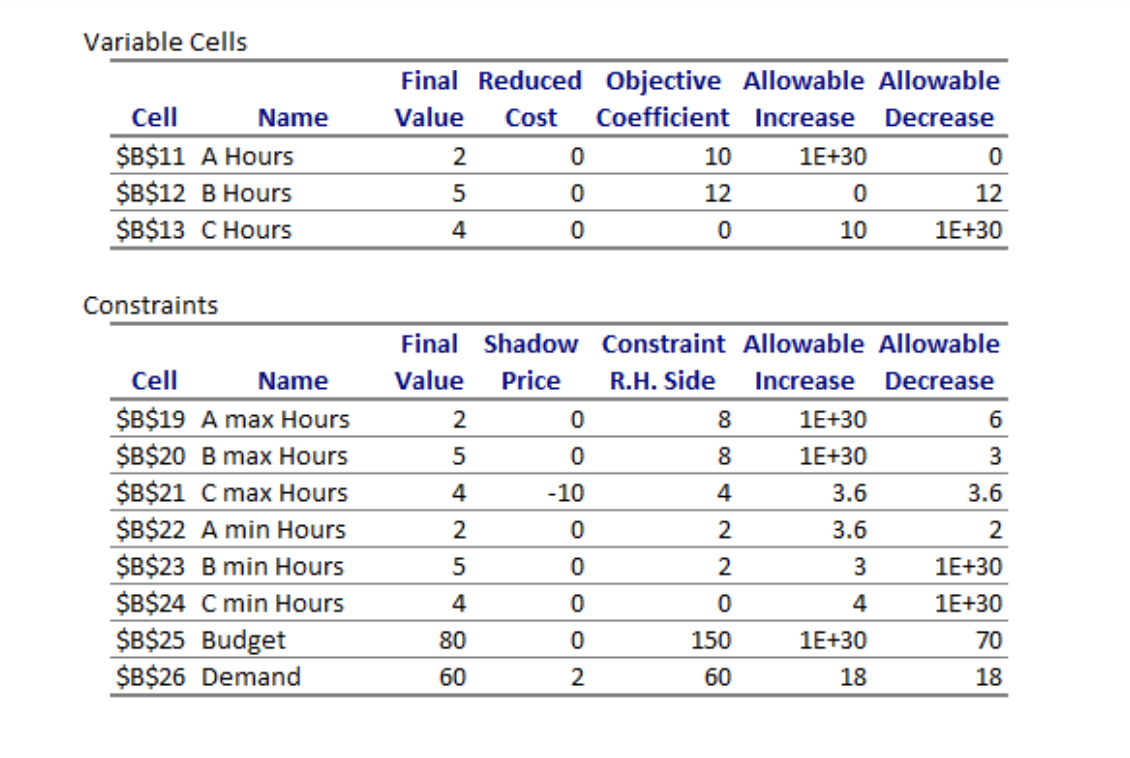
a) Based on this solution, what are the labor costs for Trojan Manufacturing, i.e., the optimal objective function value?

b) How many Trojacoins will Henry sell at that price?

c) What is the maximum revenue Henry can expect?

d) Henry decides that someday in the future, Trojacoins may be worth a lot, so he wants to keep half and sell the rest. Should he change the price at which he is willing to sell, or should he still sell at the price found in part (a)? What is his new revenue?

Worker | A B C Capacity (Widgets/hour) 5 6 5 Fred needs to determine how many hours each worker needs to work to minimize labor costs (workers can work fractions of hours) including staying under his budget of $150 per day and still meet customer demand. The formulation of the linear optimization problem is as follows: Decision Variables A = hours Worker A is asked to work per day B = hours Worker B is asked to work per day C = hours Worker C is asked to work per day Objective Function: Min 10A + 12B + OC Constraints A Max A 2 B Min B => 2 Budget 12A +10B = 60 Non-negativity A, B, C >=0 After solving a linear optimization problem, Fred comes up with the following Sensitivity Table: Variable Cells Cell Name $B$11 A Hours $B$12 B Hours $B$13 C Hours Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 2 0 10 1E+30 0 5 0 12 0 12 4 0 0 10 1E+30 Constraints Cell Name $B$19 A max Hours $B$20 B max Hours $B$21 Cmax Hours $B$22 A min Hours $B$23 B min Hours $B$24 C min Hours $B$25 Budget $B$26 Demand Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 2 0 8 1E+30 6 5 0 8 1E+30 3 4 -10 4 3.6 3.6 2 0 2 3.6 2 5 0 3 1E+30 4 0 4 1E+30 80 0 150 1E+30 70 60 2 60 ON 18 18 Worker | A B C Capacity (Widgets/hour) 5 6 5 Fred needs to determine how many hours each worker needs to work to minimize labor costs (workers can work fractions of hours) including staying under his budget of $150 per day and still meet customer demand. The formulation of the linear optimization problem is as follows: Decision Variables A = hours Worker A is asked to work per day B = hours Worker B is asked to work per day C = hours Worker C is asked to work per day Objective Function: Min 10A + 12B + OC Constraints A Max A 2 B Min B => 2 Budget 12A +10B = 60 Non-negativity A, B, C >=0 After solving a linear optimization problem, Fred comes up with the following Sensitivity Table: Variable Cells Cell Name $B$11 A Hours $B$12 B Hours $B$13 C Hours Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 2 0 10 1E+30 0 5 0 12 0 12 4 0 0 10 1E+30 Constraints Cell Name $B$19 A max Hours $B$20 B max Hours $B$21 Cmax Hours $B$22 A min Hours $B$23 B min Hours $B$24 C min Hours $B$25 Budget $B$26 Demand Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 2 0 8 1E+30 6 5 0 8 1E+30 3 4 -10 4 3.6 3.6 2 0 2 3.6 2 5 0 3 1E+30 4 0 4 1E+30 80 0 150 1E+30 70 60 2 60 ON 18 18