Question: The demand function for a certain product is 9 = f (p) =1 500 -50p where q equals the quantity demanded in thousands of units

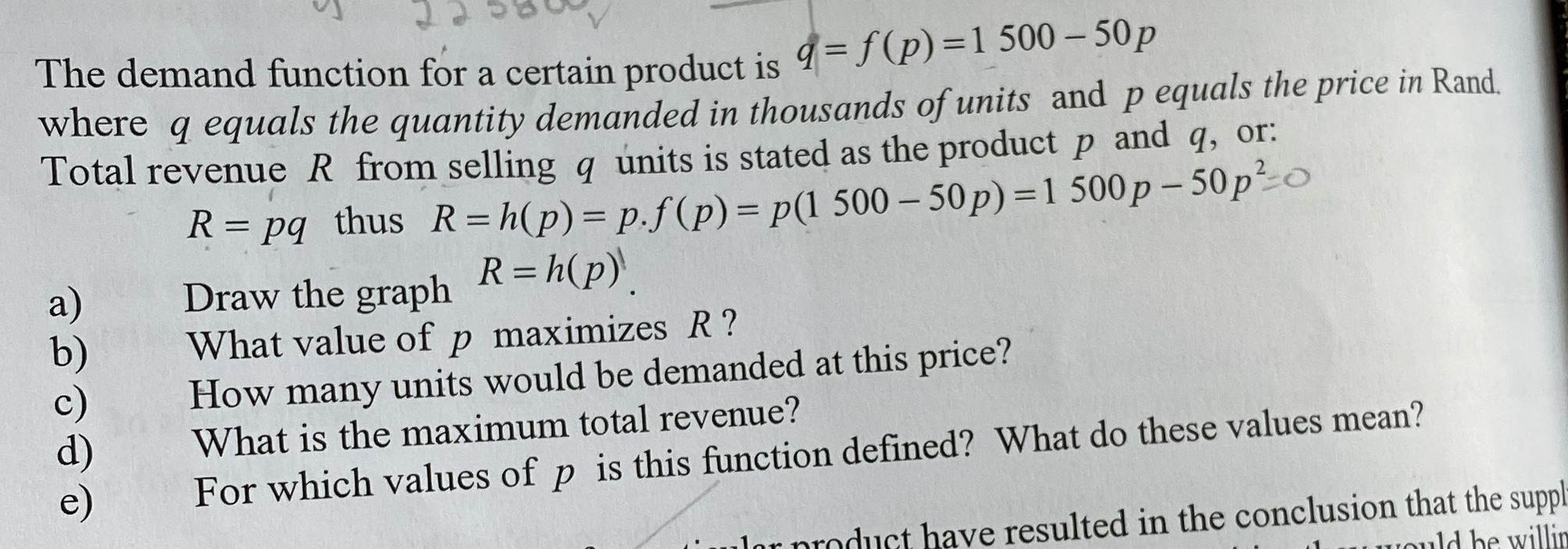
The demand function for a certain product is 9 = f (p) =1 500 -50p where q equals the quantity demanded in thousands of units and p equals the price in Rand. Total revenue R from selling q units is stated as the product p and q, or: R = pq thus R = h(p) = p.f(p) = p(1 500 -50p) =1500p - 50p2-o Draw the graph R= h(p) What value of p maximizes R? How many units would be demanded at this price? What is the maximum total revenue? For which values of p is this function defined? What do these values mean? uct have resulted in the conclusion that the suppl uld be willin

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Help kindly! (1) Michelle monopoly mutant has the exclusive right to sell mutant In the united States The demand for these tshirts is Q= 10, 000 p2 The finns shortrun cost Is SRIC= 2000 + 5Q and the...

solve all on paper ty 8. The demand funcTion for a cerTain producT is given by p: _04q+80003q520,000 where p denoTes The uniT price in dollars and q denoTes The quanTiTy demanded. a. DeTermine The...

The demand function for a certain product is given by p = 2:132 -|- 50, Where p is the unit price in dollars and x is the quantity demanded. The supply function for this product is given by p = x2 4m...

Hello, can someone help me with this question, please? The demand function for a certain product is given by p = 500 + 1000/q + 1 where rho is the price and q is the number of units demanded. Find...

Answer all questions correctly 1) For the years from 2002 and projected to 2024, the national health care Expenditures H, in billions of dollars, can be noticed by H= 1, 50De 0.053+ Where & is the...

Please answer step by step. 21. dx Assume x and y are functions of t. Evaluate % for 3xy 2x + 2y3 = 12. with the conditions 3 = - 6, x: 2, y = 1. _ dt _ (Type an exact answer in simplied form.) ID:...

The demand function for a certain product is determined by the fact that the product of the price and the quantity demanded equals 6000. The product sells fo $3.30 per unit. Suppose manufacturing...

Problem 6. An economist has estimated the demand equation of a certain product as Q=100-2.5P where P is the price unit and Q is the quantity demanded (in thousands) per year. a.Calculate and...

solve all on paper l E_xe_r'ci_ss_1 A cerTain manufacTurer esTimaTed ThaT The ToTol weekly cosT i_n producing q uniTs is C(q) = 2000 + 2q 0.0001912 (0 S q S 6000) dollars. a. WhaT is The acTual cosT...

Explain clearly. Problem 7.11. A financial institution has entered into a 10-year currency swap with company Y. Under the terms of the swap, the financial institution receives interest at 3% per...

In a recent General Social Survey, respondents answered the question, In the past month, about how many hours have you spent praying, meditating, reading religious books, listening to religious...

Suppose that you were given the following data for past excess quarterly returns for Markese Imports, Inc., and for the market portfolio: On the basis of this information, graph the relationship...

Bernard is a certified public accountant (CPA) preparing tax returns for various clients during the tax season. He takes pride in providing accurate tax advice and ensuring compliance with IRS...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...