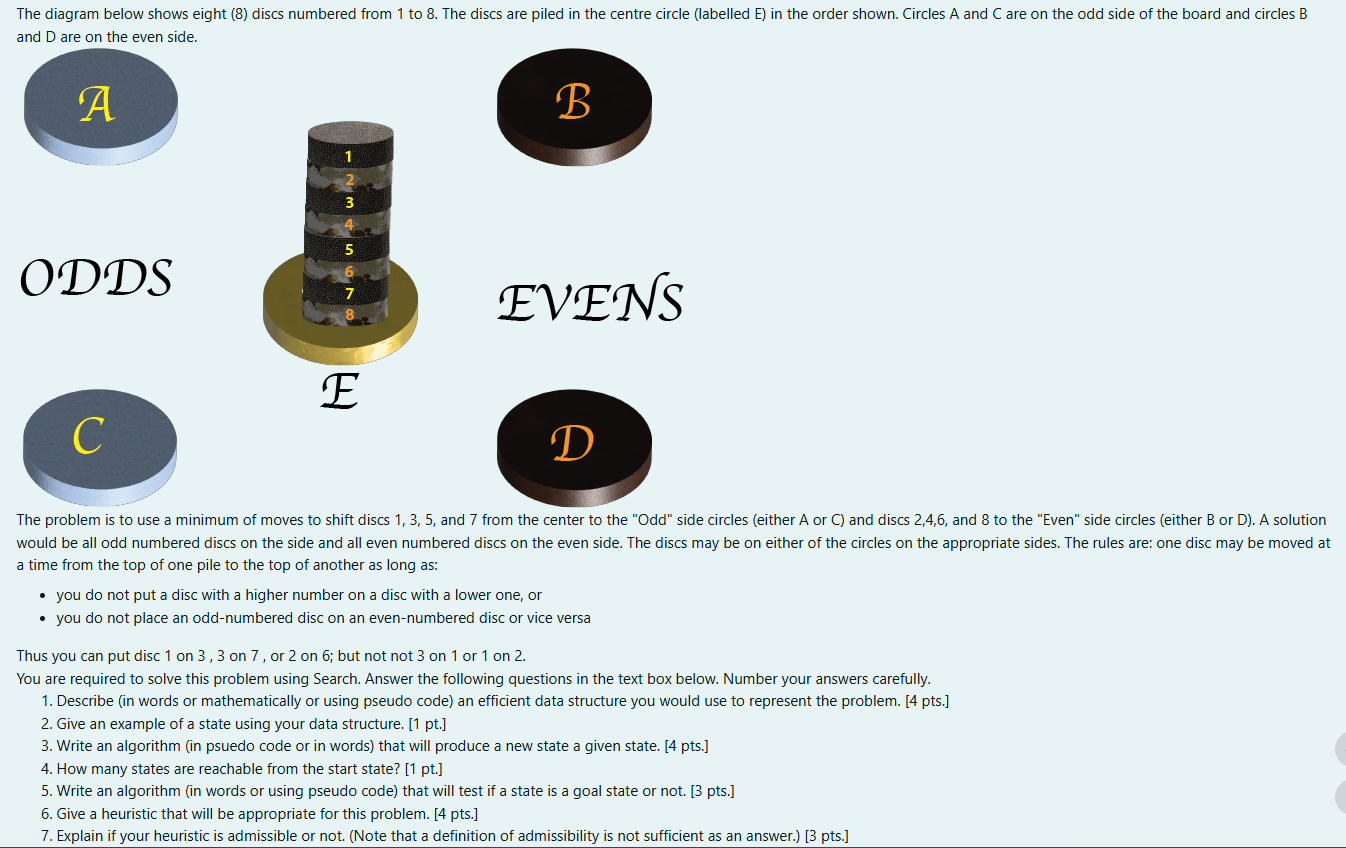
The diagram below shows eight $(8)$ discs numbered from $1$ to $8.$ The discs are piled in the centre circle $($labelled E $)$ in the order shown. Circles A and C are on the odd side of the board and circles B and $\backslash ($ D $\backslash )$ are on the even side.

The problem is to use a minimum of moves to shift discs $1,3,5,$ and $7$ from the center to the "Odd" side circles $($either A or C$)$ and discs $2,4,6,$ and $8$ to the "Even" side circles $($either B or D$).$ A solution would be all odd numbered discs on the side and all even numbered discs on the even side. The discs may be on either of the circles on the appropriate sides. The rules are: one disc may be moved at a time from the top of one pile to the top of another as long as:

$-$ you do not put a disc with a higher number on a disc with a lower one, or

$-$ you do not place an odd$-$numbered disc on an even$-$numbered disc or vice versa

Thus you can put disc $1$ on $3,3$ on $7,$ or $2$ on $6$ ; but not not $3$ on $1$ or $1$ on $2.$

You are required to solve this problem using Search. Answer the following questions in the text box below. Number your answers carefully.

$1.$ Describe $($in words or mathematically or using pseudo code$)$ an efficient data structure you would use to represent the problem. $[4$ pts$.]$

$2.$ Give an example of a state using your data structure. $[1$ pt$.]$

$3.$ Write an algorithm $($in psuedo code or in words$)$ that will produce a new state a given state. $[4$ pts$.]$

$4.$ How many states are reachable from the start state? $[1$ pt$.]$

$5.$ Write an algorithm $($in words or using pseudo code$)$ that will test if a state is a goal state or not. $[3$ pts$.]$

$6.$ Give a heuristic that will be appropriate for this problem. $[4$ pts$.]$

$7.$ Explain if your heuristic is admissible or not. $($Note that a definition of admissibility is not sufficient as an answer.$)[3$ pts$.]$