The diagram shown in Figure $2$ is a schematic representation of a film blowing die. iii. Stating your assumptions clearly, show that the velocity profile for polymer melt

A can be written as:

$v_z(r)=\frac{1}{2}\frac{\text{d}\text{e}\text{l}\text{p}}{\text{d}\text{e}\text{l}\text{z}}(\frac{r^2}{2}-(R_i{)}^{2}lnr)+c_2$

where $c_2$ is an integration constant.

iv$.$ Assuming that no slip conditions exist on both of the stationary walls of the

annulus, show that

$(R_i{)}^2=\frac{(R_i^2-R_o^2)}{2ln(\frac{R_i}{R_o})}$

and hence that the velocity profile can be written as

$v_z(r)=\frac{1}{4}\frac{\text{d}\text{e}\text{l}\text{p}}{\text{d}\text{e}\text{l}\text{z}}((r^2-R_i^2)+\frac{(R_i^2-R_o^2)}{ln(\frac{R_i}{R_o})}ln(\frac{R_i}{r}))$ v$.$ For many film blowing dies, the inner and outer radii are large enough and the annular gap is small enough for curvature to be neglected: in these cases, an excellent approximation for the velocity field in the annular gap is that for flow in a parallel$-$sided slot. A schematic diagram of such a slot is shown in Figure $3$ where the width of the slot is equal to the perimeter of the annulus.

Flow direction

Figure $3.$ Approximate flow geometry for an annulus where curvature is negligible. The velocity field in a slot of this nature can be written

$v_z(x)=\frac{1}{2}\frac{\text{d}\text{e}\text{l}\text{p}}{\text{d}\text{e}\text{l}\text{z}}(x^2-b^2)$

By making suitable substitutions for the slot half thickness, $b,$ and the $x-$

coordinate in terms of $R_i,R_0$ and $r,$ show that

$v_z(r)=-\frac{1}{2}\frac{\text{d}\text{e}\text{l}\text{p}}{\text{d}\text{e}\text{l}\text{z}}(r(R_0+R_t-r)-R_o{R}_t)$

vi$.$ In order to compare the velocity profiles from parts $($iv$)$ and $($v$)$ for different

amounts of curvature it is convenient to say that $R_i=R_0.$ Use this substitution

to compare when the result from part $($iv$)$ should be used in preference to the

simpler result from part $($ v $).$ You may find it useful to quantify the average

difference in the velocity fields and to base your judgement on that. Comment

on your answer in relation to practical design estimates.

vii. Describe how you would now check whether the initial assumption of the

range of shear rates likely to be encountered in the die is correct or not. You

need not do any calculations or derivations when answering this question.

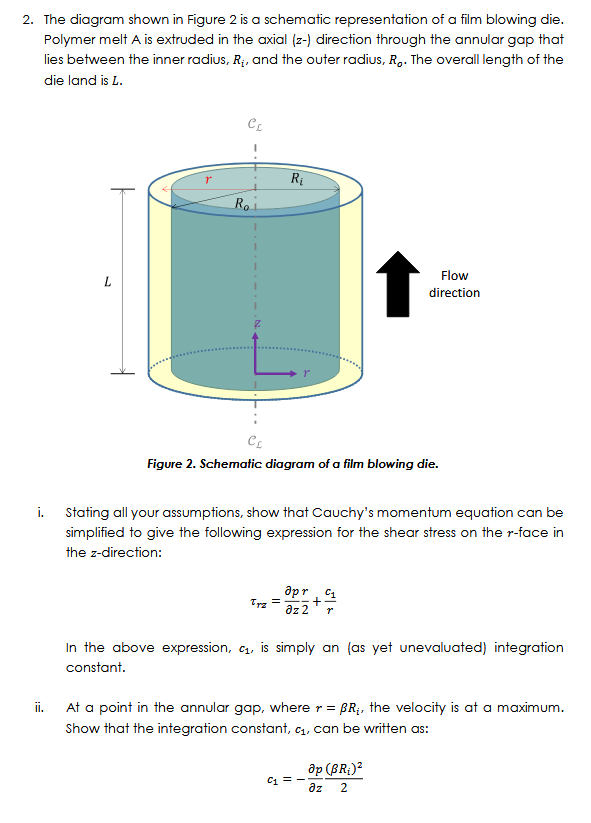
Polymer melt $A$ is extruded in the axial $(z-)$ direction through the annular gap that

lies between the inner radius, $R_i,$ and the outer radius, $R_o.$ The overall length of the

die land is $L.$

Figure $2.$ Schematic diagram of a film blowing die.

i$.$ Stating all your assumptions, show that Cauchy's momentum equation can be

simplified to give the following expression for the shear stress on the $r-$face in

the $z-$direction:

${}_{rz}=\frac{\text{d}\text{e}\text{l}\text{p}}{\text{d}\text{e}\text{l}\text{z}}\frac{r}{2}+\frac{c_1}{r}$

In the above expression, $c_1,$ is simply an $($as yet unevaluated$)$ integration

constant.

ii$.$ At a point in the annular gap, where $r=R_i,$ the velocity is at a maximum.

Show that the integration constant, $c_1,$ can be written as:

$c_1=-\frac{\text{d}\text{e}\text{l}\text{p}}{\text{d}\text{e}\text{l}\text{z}}\frac{(R_i{)}^2}{2}$