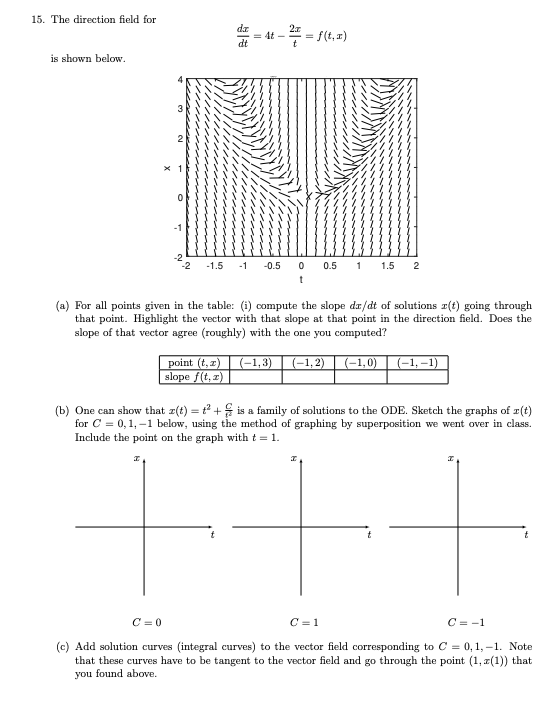
Question: The direction field for d x d t = 4 t - 2 x t = f ( t , x ) i s shown
The direction field for
shown below.
For all points given the table: compute the slope solutions going through
that point. Highlight the vector with that slope that point the direction field. Does the
slope that vector agree with the one you computed?
One can show that a family solutions the ODE. Sketch the graphs
for below, using the method graphing superposition went over class.
Include the point the graph with
Add solution curves curves the vector field corresponding
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


